Câu 2) Cho tam giác ABC, có D là điểm chính giữa của cạnh BC. Trên cạnh AC lấy điểm M sao cho AM bằng 1/3 AC. a) So sánh diện tích hai tam giác ADM và ABC b) Trên cạnh AB lấy điểm N sao cho AN = NB. Tính diện tích tam giác DMN, nếu biết diện tích tam giác ABC là 640...
Đọc tiếp
Câu 2) Cho tam giác ABC, có D là điểm chính giữa của cạnh BC. Trên cạnh AC lấy điểm M sao cho AM bằng 1/3 AC.
a) So sánh diện tích hai tam giác ADM và ABC
b) Trên cạnh AB lấy điểm N sao cho AN = NB. Tính diện tích tam giác DMN, nếu biết diện tích tam giác ABC là 640 cm2
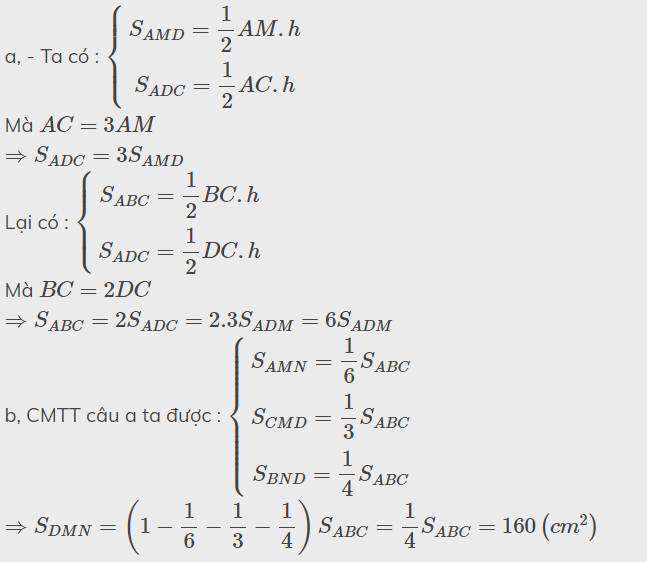
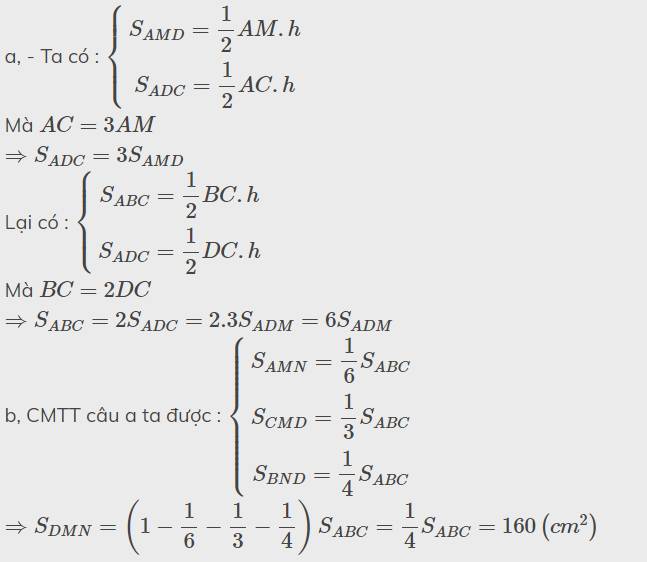
a, - Ta có : \(\left\{{}\begin{matrix}S_{AMD}=\dfrac{1}{2}AM.h\\S_{ADC}=\dfrac{1}{2}AC.h\end{matrix}\right.\)
Mà \(AC=3AM\)
\(\Rightarrow S_{ADC}=3S_{AMD}\)
Lại có : \(\left\{{}\begin{matrix}S_{ABC}=\dfrac{1}{2}BC.h\\S_{ADC}=\dfrac{1}{2}DC.h\end{matrix}\right.\)
Mà \(BC=2DC\)
\(\Rightarrow S_{ABC}=2S_{ADC}=2.3S_{ADM}=6S_{ADM}\)
b, CMTT câu a ta được : \(\left\{{}\begin{matrix}S_{AMN}=\dfrac{1}{6}S_{ABC}\\S_{CMD}=\dfrac{1}{3}S_{ABC}\\S_{BND}=\dfrac{1}{4}S_{ABC}\end{matrix}\right.\)
\(\Rightarrow S_{DMN}=\left(1-\dfrac{1}{6}-\dfrac{1}{3}-\dfrac{1}{4}\right)S_{ABC}=\dfrac{1}{4}S_{ABC}=160\left(cm^2\right)\)
Sai cách lớp 5 rồi