hình vẽ
Cho điện trở r và biến trở Rx ; hiệu điện thế nguồn là U. Xác định giá trị của Rx để công suất tiêu thụ trên nó cực đại
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tìm công suất tỏa nhiệt trên điện trở R 4
Chọn chiều dòng điện qua các điện trở trong mạch như hình vẽ.
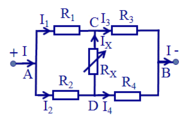
* Xét tại nút A ta có: I = I 1 + I 2 (1)
Với vòng kín ACDA ta có:
I 1 R 1 - I X R X - I 2 R 2 = 0 (2)
Thế (1) vào (2) ta được biểu thức I :
I 1 R 1 - I X R X - ( I - I 1 ) R 2 = 0 I 1 R 1 - I X R X - I R 2 + I 1 R 2 = 0 I 1 ( R 1 + R 2 ) = I X R X + I R 2 ⇒ I 1 = I X . R X + I . R 2 R 1 + R 2 = I X . R X + I . R 4 R (3)
* Xét tại nút B ta có: I 3 = I - I 4 (4)
Với vòng kín BCDB ta có:
I 3 R 3 - I X R X + I 4 R 4 = 0 I 3 R - I X R X + I 4 X = 0 (5)
Thế (4) vào (5) ta có biểu thức
I
4
:
(
I
-
I
4
)
R
-
I
X
R
X
+
I
4
R
=
0
I
.
R
+
I
4
R
-
I
X
R
X
+
I
4
R
=
0
⇒ I 4 = I . R + I X R X 2 R (6)
Từ (3) và (6) ta có: = 2 ð = =
Vậy công suất tỏa nhiệt trên R 4 khi đó là P 4 = 4 3 P 1 = 12 W .
b) Tìm R X theo R để công suất tỏa nhiệt trên R X cực đại
Từ (4) và (5) ta có biểu thức I 3 :
I 3 R - I X R X + ( I - I 3 ) R = 0 I 3 R - I X R X + I R - I 3 R = 0 ⇒ I 3 = I . R - I X R X 2 R (7)
Ta có: U = U A B = U A C + U C B = I 1 . R 1 + I 3 R 3 U = I 1 3 R + I 3 R (8)
Thế (3) và (7) vào (8) ta được:
U = I X R X + I . R 4 R . 3 R + I . R - I X R X 2 R . R 4 U = 3 . I X R X + 3 . I . R + 2 I . R - 2 I X R X 4 U = 5 . I . R + I X R X (9)
Tính I:
Ta có:
I = I 1 + I 2 = I 1 + I 4 + I X = 3 I 1 + I X = 3 . I X R X + I R 4 R + I X ⇒ 4 . I . R = 3 I X R X + 3 . I . R + 4 . I X . R ⇒ I R = 3 I X . R X + 4 . I X . R t h a y v à o ( 9 ) t a đ ư ợ c : 4 U = 5 . ( 3 I X . R X + 4 I X . R ) + I X R X = 15 . I X . R X + 20 I X R + I X R X = 16 . I X R X + 20 I X R ⇒ I X = U 4 R X + 5 R
Hai số dương 4 R x và 5 R R x có tích 4 R x . 5 R R x = 20 R không đổi thì theo bất đẳng thức Côsi, tổng của hai số đó nhỏ nhất khi hai số đó bằng nhau nghĩa là khi 4 R x = 5 R R x ⇒ R x = 1 , 25 R ; mẫu số ở vế phải của biểu thức (10) nhỏ nhất nghĩa là P X cực đại. Vậy PX cực đại khi R X = 1 , 25 R .

để đèn sáng bình thường\(=>\left\{{}\begin{matrix}U\left(đ\right)=U\left(đm\right)=6V\\I\left(đ\right)=I\left(đm\right)=0,75A\end{matrix}\right.\)\(=>R\left(đ\right)=\dfrac{U\left(đ\right)}{I\left(đ\right)}=\dfrac{6}{0,75}=8\left(om\right)\)
\(=>Im=I\left(đ\right)=0,75A\)
\(=>Rtd=\dfrac{Umn}{Im}=\dfrac{12}{0,75}=16\left(om\right)=R\left(đ\right)+Rx\)\(=>Rx=16-R\left(đ\right)=16-8=8\left(om\right)\)
Vậy.......

a, theo sơ đồ \(=>\left(Rx//R0\right)ntR\left(đ\right)\)
\(=>R\left(đ\right)=\dfrac{6^2}{6}=6\left(om\right)\)\(,I\left(đm\right)=\dfrac{P\left(đm\right)}{U\left(đm\right)}=\dfrac{6}{6}=1A\)
\(=>Rtd=R\left(đ\right)+\dfrac{Rx.R0}{Rx+R0}=6+\dfrac{2.6}{2+6}=7,5\left(om\right)\)
\(=>Im=\dfrac{UAB}{Rtd}=\dfrac{9}{7,5}=1,2A=I\left(đ\right)>I\left(đm\right)\)
=>đèn sáng hơn bình thường
\(=>P\left(đ\right)=I\left(đ\right)^2R\left(đ\right)=1,2^2.6=8,64W\)
b, khi đèn sáng bình thường\(=>\left\{{}\begin{matrix}U\left(đ\right)=U\left(đm\right)=6V\\P\left(đ\right)=P\left(đm\right)=6W\end{matrix}\right.\)\(=>Im=I\left(đ\right)=\dfrac{6}{6}=1A=Ix0\)
\(=>Ux0=Uab-U\left(đ\right)=9-6=3V\)
\(=>Rx0=\dfrac{Ux0}{Ix0}=\dfrac{3}{1}=3\left(om\right)\)
\(=>3=\dfrac{Rx.R0}{Rx+R0}< =>3=\dfrac{Rx.6}{6+Rx}=>Rx=6\left(om\right)\)
do đó phải dịch chuyển biến trở sang phải

Trước tiên, mắc R và ampe kế nối tiếp nhau và mắc vào ngồn điện có hiệu điện thế U không đổi nhưng chưa biết giá trị của U như hình vẽ.
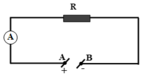
Đọc số chỉ của ampe kế lúc này ta được I
Áp dụng công thức: U = I.R ta tìm được được giá trị của U
+ Sau đó ta bỏ điện trở R ra ngoài và thay điện trở R x vào:
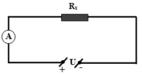
Lúc này đọc số chỉ của ampe kế ta được I x
Ta có: U =
I
x
.
R
x
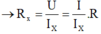 , như vậy ta tìm được giá trị của
R
x
.
, như vậy ta tìm được giá trị của
R
x
.
ta có \(Im=Ix=\dfrac{U}{\left(Rx+r\right)}\)
\(=>Px=Ix^2.Rx=\dfrac{U^2Rx}{\left(Rx+r\right)^2}=\dfrac{U^2}{\dfrac{\left(Rx+r\right)^2}{\sqrt{Rx}^2}}\)
\(=>Px=\dfrac{U^2}{\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2}\)
Px đạt cực đại <=>\(\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\) đạt Min
áp dụng bdt cosi(do Rx,r không âm)
\(=>\left(\sqrt{Rx}+\dfrac{r}{\sqrt{Rx}}\right)^2\ge4r\)
dấu"=" xảy ra<=>\(\sqrt{Rx}=\dfrac{r}{\sqrt{Rx}}< =>Rx=r\)
vậy Rx=r thì Px đạt cực đại