Tìm số tự nhiên có ba chữ số sao cho tỉ số giữa số đó với tổng các chữ số của nó là lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bai 2 so minh da giai roi minh se giai bai 3 chu so nhe no tuong tu nhu bai 2 chu so chi khac mot chut ve cach nhan xet
Goi abc la so co 3 chu so (a >0 va a,b,c<10)
Theo de bai ta co
abc: (a+b+c) co gia tri nho nhat
Phan h cau tao so
abc = 100a +10b + c = 10(a+b+c) + 90a -9c
( Thêm vao 9xc va bớt ra 9xc)
thay the vao ta co
(10x(a+b+c) + 9(10a-c) ) : (a+b+c) = 10 + 9(10a-c) : ( a+b+c)
Nhan xet : 10 + 9(10a - c) : (a+b+c) dat gia tri nho nhat khi 9x(10a-c) : (a+b+c) dat gia tri lon nhat vi so 10 la khong thay doi
Xet phan so 9x(10a-c) : (a+b+c) phai dat gia tri nho nhat ma phai la so nguyen vay chi co the la tu so bang mau so
9x(10a-c) = a+b+c
gia su a , b,c nhan gia tri lon nhat va de bang 9
9+9+9 =27
suy ra 9x(10a-c) < 28
ta co 10a- c phải nho hơn 4 vi nếu bằng 4 thi 9x4 =36>27
Hiẹu 10a-c < 4 khi a bang 1 moi thoa dieu kien
thay vao phan so dang xet
9(10-c) = 1 + b+ c
90-9c =1+b+c
----> 10c = 89-b
de hieu 89-c chia het cho 10 thi hang don vi cua hieu do phai bang 0
Vậy : 9-b=0 <----> b = 9
----> c = (89-9) : 10 = 8
Kết luận de phân so abc : (a+b+c) dat gia tri nho nhat khi
a = 1, b = 9, c = 8
DS : so can tim de phan so co 3 chu so dat gia tri nho nhat la 198
ban lam tuong tu nhu phan tren de tim phan so co 3 chu so dat gia tri lon nhat nhe chuc ban thanh cong

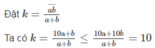
k = 10 ⇔ b = 10b ⇔ b = 0
Như vậy k lớn nhất bằng 10 ứng với các số 10; 20; 30; …; 90.

1)Gọi a và b lần lượt là chữ số hàng chục và hàng đơn vị của số đó.Vậy số đó là 10a+b (a,b là số tự nhiên nhỏ hơn 10 và a#0).
(10a+b)/(a+b)=(10a+10b-9b)/(a+b)=
=10-9b/(a+b).
Hiệu này lớn nhất bằng 10 khi b=0 (a tùy ý)

vì là lớn nhất nên các tổng phải là bé nhất để tỉ số lớn nhất nên ta hạ b=0 ta có các số
ta có 20,30,40,50,60,70,80,90

Gọi số cần tìm là \(ab\)
Đặt \(k=\frac{ab}{a+b}=\frac{10a+b}{a+b}\) nhỏ hơn hoặc bằng \(\frac{10a+10b}{a+b}=10\)
=> Vậy , \(k\) lớn nhất \(=10\) ứng với các số :\(10;20;30;40;...90\)
* Tìm số tự nhiên có hai chữ số sao cho tỉ số giữa số đó với tổng các chữ số của nó là lớn nhất.?
Gọi a là chữ số hàng chục và b là chữ số hàng đơn vị của số đó. Vậy số đó là 10a+b (a,b là số tự nhiên nhỏ hơn 10 và a # 0).
Theo đề bài ta có: (10a + b)/(a + b) = [10(a + b) - b]/(a + b) = 10 - b/(a + b)
=> số đó lớn nhất khi b/(a + b) nhỏ nhất
=> b nhỏ nhất
=> b = 0 ; a tùy ý
=> Các số cần tìm: 10; 20; 30; 40; 50; 60; 70; 80; 90.
* Tìm số tự nhiên có hai chữ số sao cho tỉ số giữa số đó với tổng các chữ số của nó là nhỏ nhất.?
Gọi a là chữ số hàng chục và b là chữ số hàng đơn vị của số đó. Vậy số đó là 10a+b (a,b là số tự nhiên nhỏ hơn 10 và a # 0).
Theo đề bài ta có: (10a + b)/(a + b) = [10(a + b) - b]/(a + b) = 10 - b/(a + b)
=> số đó nhỏ nhất khi b/(a + b) lớn nhất
=> b lớn nhất
=> b = 9 ; a tùy ý
=> Các số cần tìm: 19; 29; 39; 49; 59; 69; 79; 89; 99.
ko chắc lắm
Gọi P = \(\frac{\overline{abc}}{a+b+c}=\frac{a.100+b.10+c}{a+b+c}=\frac{a+b+c+a.99+b.9}{a+b+c}=1+\frac{a.99+b.9}{a+b+c}\)
Với a xác định, b xác định và để P lớn nhất, => c bé nhất, => c = 1
Thay vào ta có:
P= \(1+\frac{a.99+b.9}{a+b+1}=1+\frac{9.\left(a.11+b\right)}{a+b+1}=1+\frac{9.a+9.b+9}{a+b+1}+\frac{90.a-9}{a+b+1}=\)
P =\(1+\frac{9.a+9.b+9}{a+b+1}+\frac{9.\left(10.a-1\right)}{a+b+1}=1+\frac{9.\left(a+b+1\right)}{a+b+1}+\frac{9.\left(10.a-1\right)}{a+b+1}=1+9+\frac{9.\left(10.a-1\right)}{a+b+1}\)
P = \(10+\frac{9.\left(10.a-1\right)}{a+b+1}\)
Với a xác định và để P lớn nhất
=> b nhỏ nhất, => b = 1
Thay vào ta có:
P = \(10+\frac{90.a-9}{a+2}=10+\frac{90.a+180}{a+2}-\frac{189}{a+2}=10+\frac{90.\left(a+2\right)}{a+2}-\frac{189}{a+2}\)
P = \(100-\frac{189}{a+2}\)
Để P lớn nhất
=> a lớn nhất
=> a = 9
=> abc = 911
HEllo