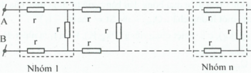
Một mạch điện như hình bên. Các điện trở như nhau và giá trị mỗi điện trở là r = 1Ω. Tính điện trở tương đương của...
Đọc tiếp
Một mạch điện như hình bên. Các điện trở như nhau và giá trị mỗi điện trở là r = 1Ω. Tính điện trở tương đương của mạch.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
17 tháng 5 2019
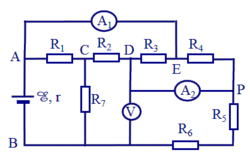
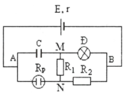
Ta có: R 34 = R 3 . R 4 R 3 + R 4 = 2 . 2 2 + 2 = 1 ( Ω ) ; R 56 = R 5 + R 6 = 2 Ω ;
Ta nhận thấy: R 1 R 34 = R 7 R 56 = 2
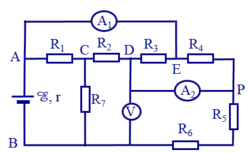
Đây là mạch cầu cân bằng, nên I 2 = 0 ; U C D = 0 , do đó có thể chập hai điểm C, D làm một khi tính điện trở.
R 134 = R 1 . R 34 R 1 + R 34 = 2 . 1 2 + 1 = 2 3 Ω ; R 567 = R 56 . R 7 R 56 + R 7 = 2 . 4 2 + 4 = 4 3 Ω ; R A B = R 134 + R 567 = 2 3 + 4 3 = 2 Ω .
b) Cường độ dòng điện qua các điện trở
Áp dụng định luật Ôm cho toàn mạch ta có: I = E R A B + r = 9 2 + 1 = 3 ( A ) ;
U A C = I . R 134 = 3 . 2 3 = 2 ( V ) ; U C D = I . R 567 = 3 . 4 3 = 4 ( V ) ;
Cường độ dòng điện qua các điện trở:
I 1 = U A C R 1 = 2 2 = 1 ( A ) ; I 3 = U A C R 3 = 2 2 = 1 ( A ) ; I 4 = U A C R 4 = 2 2 = 1 A ; I 5 = I 6 = U C B R 56 = 4 2 = 2 A ; I 7 = U C B R 7 = 4 4 = 1 A .
c) Số chỉ của các ampe kế và vôn kế
Số chỉ của vôn kế: U V = U C B = 4 V
Số chỉ của các ampe kế: I A 1 = I - I 1 = 3 - 1 = 2 A ; I A 2 = I 3 = 1 A .
VT
16 tháng 7 2019
Gọi R là điện trở tương đương của toàn mạch.Vì mạch điện có nhiều nhóm giống nhau nên nếu không kể nhóm (1) thì điện trở toàn mạch xem như cũng không đổi, nghĩa là vẫn bằng R. Ta có mạch điện tương đương như hình vẽ.
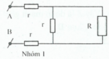
R = 2 r + R r R + r ⇒ R 2 − 2 r R − 2 r 2 = 0 ⇒ Δ ' = b ' 2 − a c = 3 r 2 R = − b ' + r 3 = r + r 3 = r 1 + 3
VT
2 tháng 7 2017
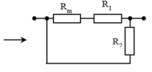
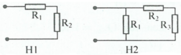
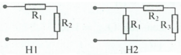
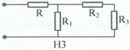
Hình 2: Vì R 2 và R 3 mắc nối tiếp nên ta có: R 23 = R 2 + R 3 = 24 Ω
Vì R 1 mắc song song với R 23 nên 1 R t d = 1 R 1 + 1 R 23 ⇒ R t d = R 1 R 23 R 1 + R 23 = 8 Ω
Chọn A
VT
2 tháng 8 2018
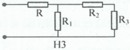
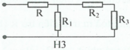
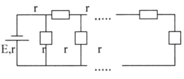
Hình 3: Vì R 2 và R 3 mắc nối tiếp nên ta có: R 23 = R 2 + R 3 = 24 Ω
Vì R 1 mắc song song với R 23 nên: 1 R 1 − 23 = 1 R 1 + 1 R 23 ⇒ R 1 − 23 = R 1 R 23 R 1 + R 23 = 8 Ω
Vì R mắc nối tiếp với R 1 - 23 nên: R t d = R + R 1 − 23 = 12 + 8 = 20 Ω
Chọn D
VT
29 tháng 12 2019
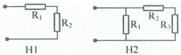
Hình 1: Vì R1 và R2 mắc nối tiếp nên ta có: R t d = R 1 + R 2 = 24 Ω
Chọn D
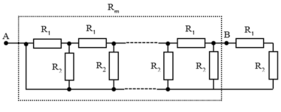
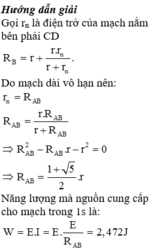
\(R_{78}=R_7+R_8=1+1=2\left(\text{Ω}\right)\)
\(R_{678}=\dfrac{R_6\cdot R_{78}}{R_6+R_{78}}=\dfrac{1\cdot2}{1+2}=\dfrac{2}{3}\left(\text{Ω}\right)\)
\(R_{5678}=R_5+R_{678}=1+\dfrac{2}{3}=\dfrac{5}{3}\left(\text{Ω}\right)\)
\(R_{45678}=\dfrac{R_4\cdot R_{5678}}{R_4+R_{5678}}=\dfrac{1\cdot\dfrac{5}{3}}{1+\dfrac{5}{3}}=\dfrac{5}{8}\left(\text{Ω}\right)\)
\(R_{345678}=R_3+R_{45678}=1+\dfrac{5}{8}=\dfrac{13}{8}\left(\text{Ω}\right)\)
\(R_{2345678}=\dfrac{R_2\cdot R_{345678}}{R_2+R_{345678}}=\dfrac{1\cdot\dfrac{13}{8}}{1+\dfrac{13}{8}}=\dfrac{13}{21}\left(\text{Ω}\right)\)
\(R_{AB}=R_1+R_{2345678}=1+\dfrac{13}{21}=\dfrac{34}{21}\left(\text{Ω}\right)\)