Cho ∆ABC,đg cao BE và CF cắt nhau tạj H .M là T điểm BC,N là tđ EF,P là tđ AH.c/m M,N,P thắng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 7 2023
a: Gọi giao của AH với BC là M
=>AH vuông góc BC tại M
góc AFH=góc AEH=90 độ
=>AEHF nội tiếp đường tròn đường kính AH
=>IF=IA=IE=IH
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp đường tròn đường kính BC
=>KF=KE=KB=KC
góc IFH+góc KFH
=góc IHF+góc KCH
=góc KCH+90 độ-góc KCH=90 độ
=>FK vuông góc FI
b: FI=AH/2=3cm
FK=BC/2=4cm
=>IK=căn 3^2+4^2=5cm
UI
9 tháng 8 2019
De bai sai roi phai la cm M,N,P thang hang moi dung
Noi PF,PE , FM EM
xet tam giac AFH vuong tai F va tam giac AEH vuong tai E deu co P la trung diem canh huyen AH (gt)
=> PF =PE (=1/2 AH) => P \(\in\) trung truc EF (1)
xet tam giac BFC vuong tai F va tam giac EBC vuong tai E cung deu co M la trung diem canh huyen BC (gt)
=> FM = ME ( = 1/2 BC ) => M\(\in\) trung truc EF (2)
Lai co N la trung diem EF (gt) (3)
tu (1),(2),(3) => M,N,P thang hang DPCM
Chuc ban hoc tot !
26 tháng 5 2020
hiiiiiiiiiiiiiiiii bn ccccccccccccccccos kkkkkkkkkkkkkkecdjfv cdsjx snbc hgcduvskla
24 tháng 8 2021
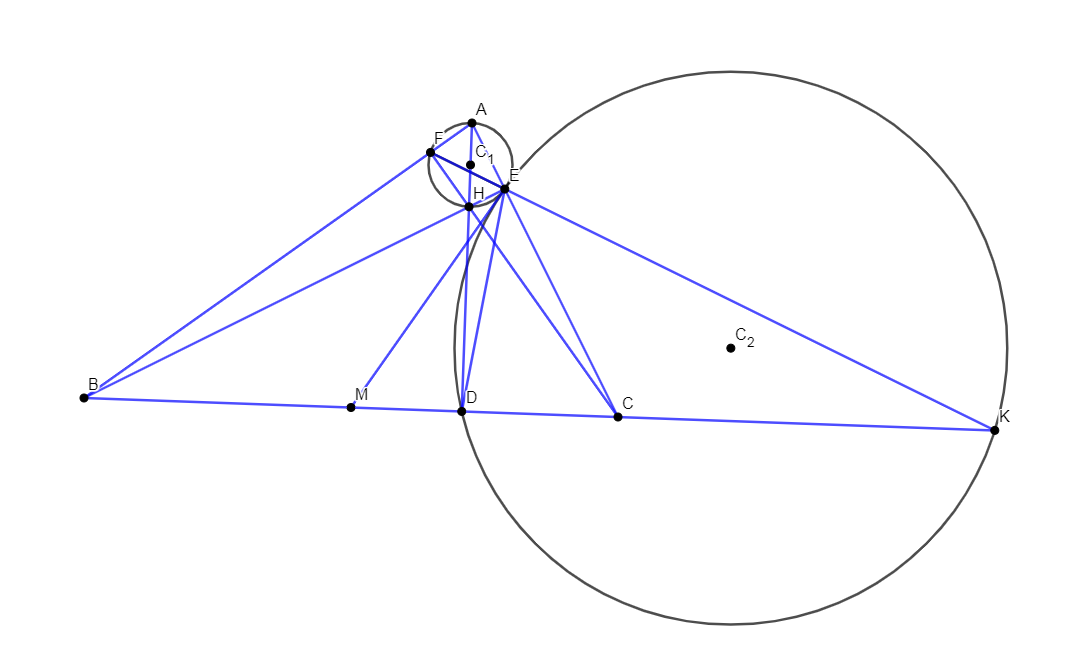
Có \(\Delta ECB\) vuông tại E và có EM là đường trung tuyến
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\)
\(\Rightarrow\Delta EBM\) cân tại M
\(\Rightarrow\widehat{BEM}=\widehat{MBE}\)
mà \(\widehat{MBE}=\widehat{CAD}\) (vì cùng phụ góc BCA)
\(\Rightarrow\widehat{BEM}=\widehat{CAD}\)
\(\Rightarrow\)EM là tiếp tuyến của (C1)
CM tương tự đc EM là tiếp tuyến của (C2)