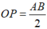cho nửa đường tròn đường kính AB. Trên đó lấy các điểm C và D sao cho AC=CD=2\(\sqrt{5}\) cm còn DB= 6 cm. Tìm bán kính của nửa đường tròn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2016
Từ O kẻ OH và OK vuông góc với BD . Nối OC , cắt AD tại K => OC vuông góc với AD (cung AC và CD bằng nhau)
Dễ thấy OHDK là hình chữ nhật => \(OK=DH=\frac{1}{2}BD=3\left(cm\right)\)
và \(DK=OH=\sqrt{OB^2-3^2}=\sqrt{r^2-9}\) (1)
Mặt khác, ta lại có \(KD=\sqrt{CD^2-KC^2}=\sqrt{20-\left(r-3\right)^2}\) (2)
Từ (1) và (2) ta có : \(\sqrt{r^2-9}=\sqrt{20-\left(r-3\right)^2}\Leftrightarrow\orbr{\begin{cases}r=5\left(n\right)\\r=-2\left(l\right)\end{cases}}\)
Vậy bán kính của dường tròn là 5 cm.
13 tháng 12 2016
Ta có
\(CB^2=CD^2+DB^2-2.CD.DB.\cos\left(\widehat{CDB}\right)\)
\(=20+36-2.2\sqrt{5}.6.\cos\left(\pi-\widehat{CAB}\right)\)
\(=56+\frac{24\sqrt{5}.2\sqrt{5}}{2R}=56+\frac{120}{R}\left(1\right)\)
Ta lại có
\(CB^2+AC^2=AD^2+DB^2=4R^2\)
\(\Leftrightarrow56+\frac{120}{R}+20=4R^2\)
\(\Leftrightarrow4R^2-\frac{120}{R}-76=0\)
\(\Leftrightarrow R^3-19R-30=0\)
\(\Leftrightarrow\left(R-5\right)\left(R+2\right)\left(R+3\right)=0\)
\(\Leftrightarrow R=5\)
12 tháng 9 2019
https://olm.vn/hoi-dap/detail/66015664055.html bạn vào đây tham khảo nha
5 tháng 3 2016
Bạn tự vẽ hình
1. Gọi \(K\) là điểm chính giữa của nửa đường tròn. Xét hai tam giác \(\Delta KOD\) và \(\Delta OCH\) có \(OK=CO=R\), \(\angle KOD=\angle OCH\) (so le trong) và \(OD=CH\) (giả thiết). Suy ra hai tam giác \(\Delta KOD\) và \(\Delta OCH\)
bằng nhau (c.g.c). Do đó \(\angle KDO=90^{\circ}\to D\) nằm trên đường tròn đường kính OK.
Khi C trùng A thì D trùng với O và khi C trùng với B thì D trùng với O. Do đó tập hợp D sẽ là toàn bộ đường tròn đường kính OK.
2. Kéo dài tia DC cắt (O) ở điểm thứ hai T. Do tứ giác ACTB nội tiếp nên góc TBA = góc DCA = 60 độ. Vậy T là điểm cố định. Do tam giác ACD đều và M là trung điểm CD nên AM vuông góc với CD. Suy ra M nhìn đoạn AT dưới 1 góc vuông. Vậy M nằm trên đường tròn đường kính AT.
Vì C chỉ chạy trên nửa đường tròn, khi C trùng A thì M trùng A và khi C trùng với B thì M trùng với T. Vậy M chạy trên nửa đường tròn đường kính AT, trong nửa mặt phẳng không chứa điểm B.
Chỉ vậy thôi.
PN
6 tháng 10 2017
Cho hình vẽ:
Từ O kẻ OK vuông góc với BD. Nối OC, cắt AD tại K \(\Rightarrow\)OC vuông góc với AD
Dễ thấy OHDK là hình chữ nhật \(\Rightarrow OK=DH=\frac{1}{2}BD=3cm\)
Và \(DK=OH=\sqrt{OB^2-3^2}=\sqrt{r^2-9}\)1
Mặt khác, ta lại có: \(KB=\sqrt{CD^2-KC^2}=\sqrt{20-r-3^2}\)2
Từ 1 và 2 ta có: \(\sqrt{r^2-9}=\sqrt{20-r-3^2}\Leftrightarrow\orbr{\begin{cases}r=5n\\r=-2l\end{cases}}\)
Vậy bán kính của đường tròn là 5 cm
CM
24 tháng 4 2017
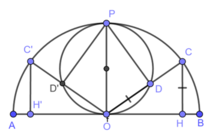
*Chứng minh thuận:
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P.
Vì O cố dịnh, đường tròn đường kính AB cố định nên P cố định.Nối PD
Ta có: OP // CH (cùng ⊥ AB)
Xét hai tam giác HCO và DOP ta có:
OD = CH (gt)
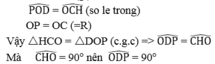
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với hai đầu đọan thẳng OP cố định một góc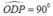 
Vậy D chuyển động trên đường tròn đường kính OP
*Chứng minh đảo
Lấy điểm D’ bất kì trên đường tròn đường kính OP ,nối OD’ cắt nửa đường tròn đường kính AB tại C’.Nối PD’ và C’H’ ⊥ AB
Xét hai tam giác C’H’O và PD’O ta có:
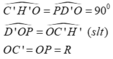
Vậy △ C’H’O = △ PD’O (c.g.c) ⇒ C’H’ = OD’
Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với 