Giải giúp mình với
√(1 - √5 )^2 phần √75
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 9 2021
d: \(\dfrac{1}{27}:\left(-\dfrac{1}{3}\right)^2+75\%\cdot\left(-\dfrac{2^2}{3}\right)\)
\(=\dfrac{1}{27}:\dfrac{1}{9}+\dfrac{3}{4}\cdot\dfrac{-4}{3}\)
\(=\dfrac{1}{3}-1\)
\(=-\dfrac{2}{3}\)
8 tháng 2 2019
a) = ( 9/10 - 4/5) + ( 3/4 + 1/2)
= ( 9/10 - 8/10) + ( 3/4 + 2/4)
= 1/10 + 5/4
= 2/20 + 25/20 = 27/20
b) = (4/5 + 4/15) + (5/6 - 1/2)
= (12/15 - 4/15) + (5/6 - 3/6)
= 8/15 + 2/6
= 16/30 + 10/30
= 26/30 = 13/15
c) = 55 - 39 - 1 + 60 /75 = 75/75 = 1
d) = 47 + 35 - 36 + 15/42 = 61/42
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
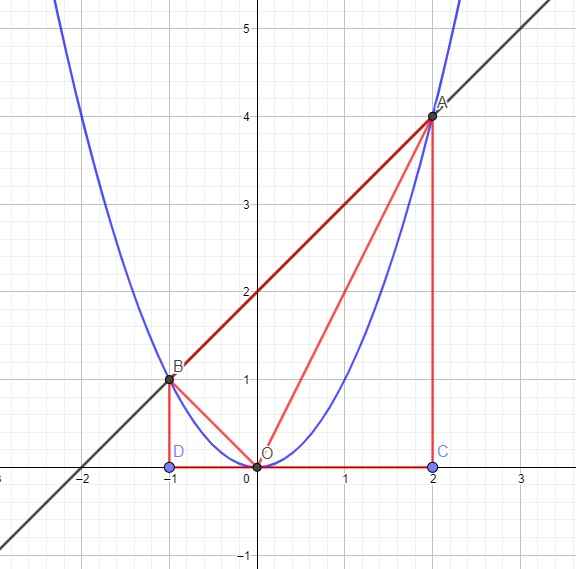
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
S
2 tháng 3 2017
\(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{999\times1000}+1\)
\(=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+....+\frac{1}{999000}+1\)
\(=1-\frac{1}{1000}+1\)
\(=\frac{1999}{1000}\)
PT
4 tháng 2 2019
\(\frac{75}{100}+\frac{3}{4}x29+75\%x30+0,75x40\)
\(=\frac{3}{4}+\frac{3}{4}x29+\frac{75}{100}x30+\frac{75}{100}x40\)
\(=\frac{3}{4}+\frac{3}{4}x29+\frac{3}{4}x30+\frac{3}{4}x40\)
\(=\frac{3}{4}x\left(1+29+30+40\right)\)
\(=\frac{3}{4}x100\)
= 75