1,tính
a,1+5+9+............+n+(n+1)+(n+2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 11 2023
a: \(\lim\limits_{n\rightarrow+\infty}\dfrac{n^5+n^2-n+2}{\left(2n^3-1\right)\left(n^2+n+1\right)}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{1+\dfrac{1}{n^3}-\dfrac{1}{n^4}+\dfrac{2}{n^5}}{\left(\dfrac{2n^3}{n^3}-\dfrac{1}{n^3}\right)\left(\dfrac{n^2+n+1}{n^2}\right)}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{1+\dfrac{1}{n^3}-\dfrac{1}{n^4}+\dfrac{2}{n^5}}{\left(2-\dfrac{1}{n^3}\right)\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}\right)}\)
\(=\dfrac{1}{2\cdot1}=\dfrac{1}{2}\)
b: \(\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt{n^2-n+2}}{n+2}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n\sqrt{1-\dfrac{1}{n}+\dfrac{2}{n^2}}}{n\left(1+\dfrac{2}{n}\right)}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt{1-\dfrac{1}{n}+\dfrac{2}{n^2}}}{1+\dfrac{2}{n}}=\dfrac{\sqrt{1-0+0}}{1+0}=\dfrac{1}{1}=1\)
c: \(\lim\limits_{n\rightarrow+\infty}\dfrac{n-\sqrt[3]{n^2-n^3}}{n^2+n+1}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{\dfrac{n}{n^2}-\dfrac{\sqrt[3]{n^2-n^3}}{n^2}}{1+\dfrac{1}{n}+\dfrac{1}{n^2}}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{\dfrac{1}{n}-\sqrt[3]{\dfrac{1}{n^4}-\dfrac{1}{n^3}}}{1+\dfrac{1}{n}+\dfrac{1}{n^2}}=\dfrac{0}{1}=0\)
d: \(\lim\limits_{n\rightarrow+\infty}\left(n-\sqrt{n^2+n+1}\right)\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n^2-n^2-n-1}{n+\sqrt{n^2+n+1}}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{-n-1}{n+\sqrt{n^2+n+1}}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{-1-\dfrac{1}{n}}{1+\sqrt{1+\dfrac{1}{n}+\dfrac{1}{n^2}}}=-\dfrac{1}{1+1}=-\dfrac{1}{2}\)
24 tháng 11 2023
\(\lim\limits_{n\rightarrow+\infty}\left(\sqrt[3]{n^3+n^2+n+1}-n\right)\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n^3+n^2+n+1-n^3}{\sqrt[3]{\left(n^3+n^2+n+1\right)^2}+n\cdot\sqrt[3]{n^3+n^2+n+1}+n}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n^2+n+1}{\sqrt[3]{\left[n^3\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}\right)\right]^2}+n^2\cdot\sqrt[3]{1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}}+n^2}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n^2+n+1}{n^2\cdot\sqrt[3]{\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}\right)^2}+n^2\cdot\sqrt[3]{1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}}+n^2}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{1+\dfrac{1}{n}+\dfrac{1}{n^2}}{\sqrt[3]{\left(1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}\right)^2+\sqrt[3]{1+\dfrac{1}{n}+\dfrac{1}{n^2}+\dfrac{1}{n^3}}+1}}\)
\(=\dfrac{1}{1+1+1}=\dfrac{1}{3}\)
b: \(\lim\limits_{n\rightarrow+\infty}\left(\sqrt{n^2+n}-\sqrt{n^2-n+1}\right)\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{n^2+n-n^2+n-1}{\sqrt{n^2+n}+\sqrt{n^2-n+1}}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{2n-1}{\sqrt{n^2+n}+\sqrt{n^2-n+1}}\)
\(=\lim\limits_{n\rightarrow+\infty}\dfrac{2-\dfrac{1}{n}}{\sqrt{1+\dfrac{1}{n}}+\sqrt{1-\dfrac{1}{n}+\dfrac{1}{n^2}}}=\dfrac{2}{\sqrt{1}+\sqrt{1}}=1\)
27 tháng 8 2021
`a)5/9:(1/11-5/22)+5/9:(1/15-2/3)`
`=5/9:(2/22-5/22)+5/9:(1/15-10/15)`
`=5/9:(-3)/22+5/9:(-9)/15`
`=5/9*(-22)/3+5/9*(-5)/3`
`=5/9*(-22/3+(-5)/3)`
`=5/9*(-9)=-5`
BH
2
5 tháng 2 2022
a \(\dfrac{53}{84}\)
b \(\dfrac{20}{63}\)
c \(\dfrac{1}{60}\)
5 tháng 2 2022
a: \(\dfrac{2}{3}+\dfrac{5}{7}-\dfrac{3}{4}=\dfrac{56}{84}+\dfrac{60}{84}-\dfrac{63}{84}=\dfrac{53}{84}\)
b: \(=\dfrac{3}{7}-\dfrac{1}{9}=\dfrac{27}{63}-\dfrac{7}{63}=\dfrac{20}{63}\)
c: \(=\dfrac{2}{5}\cdot\dfrac{1}{8}\cdot\dfrac{1}{3}=\dfrac{2}{8}\cdot\dfrac{1}{15}=\dfrac{1}{60}\)
KA
4
TH
31 tháng 1 2021
a) 1-3+5-7+9-12+15-18
= (1+ 9) - (3+7) + (5+15) - (12+18)
= 10 - 10 + 20 - 30 = -10.
b) (-2)+5-7+9-11+13-15+19-21
= 5 - 11 - 2 -2 = 5 - (11+2+2)
= 5 - 15 = -10
31 tháng 1 2021
Bài 1:
a) Ta có: 1-3+5-7+9-12+15-18
=(1+9)-(3+7)+(5+15)-(12+18)
=10-10+20-30
=-10
b) Ta có: \(\left(-2\right)+5-7+9-11+13-15+19-21\)
\(=3+2+2+4-21\)
\(=5+6-21\)
=11-21=-10
16 tháng 9 2023
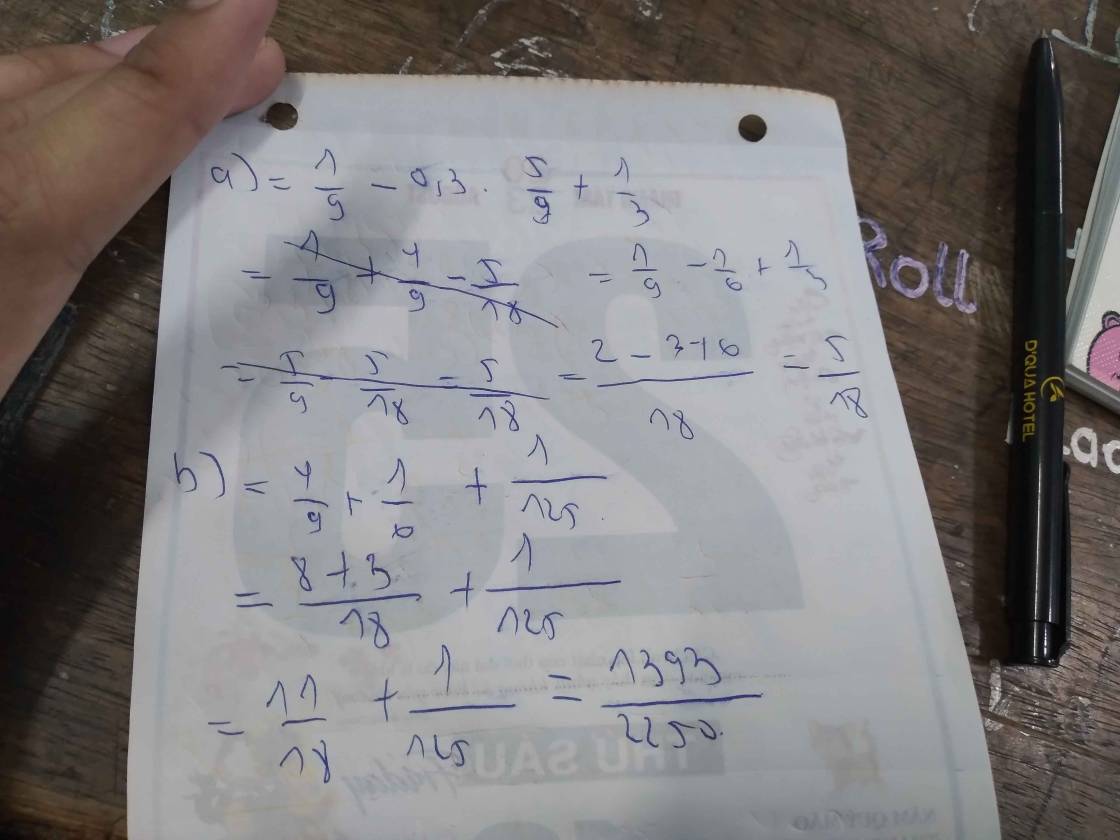
a) `1/9-0,3. 5/9+1/3`
`=1/9-3/10 . 5/9+1/3`
`=1/9-15/90+1/3`
`=1/9-1/6+1/3`
`=2/18-3/18+6/18`
`=5/18`
b) `(-2/3)^2+1/6-(-0,5)^3`
`=4/9+1/6-(-0,125)`
`=4/9+1/6+0,125`
`=4/9+1/6+1/8`
`=32/72+12/72+9/72`
`=53/72`
20 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`1,`
`a)`
`-7/25 + (-8)/25`
`= (-7 - 8)/25`
`= -15/25`
`= -3/5`
`b)`
`6/13 + (-15)/39`
`= 18/39 + (-15)/39`
`= (18 - 15)/39`
`= 3/39`
`= 1/13`
`c)`
`5/7 + 4/(-14)`
`= 10/14 + (-4)/14`
`= (10 - 4)/14`
`= 6/14`
`= 3/7`
`d)`
`-8/18 + (-15)/27`
`= -4/9 + (-5)/9`
`= (-4-5)/9`
`= -9/9 = -1`
NN
20 tháng 7 2023
`2,`
`a)`
`3/5 + (-7)/4`
`= 12/20 + (-35)/20`
`= (12 - 35)/20`
`=-23/20`
`b)`
`(-2) + (-5)/8`
`= (-16)/8 + (-5)/8`
`= (-16 - 5)/8`
`= -21/8`
`c)`
`1/8 + (-5)/9`
`= 9/72 + (-40)/72`
`= (9-40)/72`
`= -31/72`
`d)`
`6/13 + (-14)/39`
`= 18/39 + (-14)/39`
`= (18 - 14)/39`
`= 4/39`
`e)`
`(-18)/24 + 15/21`
`= (-3)/4 + 5/7`
`= (-21)/28 + 20/28`
`= (-21 + 20)/28`
`= -1/28`
22 tháng 9 2021
Bài 3:
a: Ta có: \(3x^2=75\)
\(\Leftrightarrow x^2=25\)
hay \(x\in\left\{5;-5\right\}\)
b: Ta có: \(2x^3=54\)
\(\Leftrightarrow x^3=27\)
hay x=3
22 tháng 9 2021
Bài 2:
b: Ta có: \(30-3\cdot2^n=24\)
\(\Leftrightarrow3\cdot2^n=6\)
\(\Leftrightarrow2^n=2\)
hay n=1
c: Ta có: \(40-5\cdot2^n=20\)
\(\Leftrightarrow5\cdot2^n=20\)
\(\Leftrightarrow2^n=4\)
hay n=2
d: Ta có: \(3\cdot2^n+2^n=16\)
\(\Leftrightarrow2^n\cdot4=16\)
\(\Leftrightarrow2^n=4\)
hay n=2