tìm giá trị nhỏ nhất của biểu thức:
A=x4+3x2+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
WS
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 12 2021
\(A=2\left(x^2-2xy+y^2\right)+\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{8067}{4}\)
\(A=2\left(x-y\right)^2+\left(x-\dfrac{3}{4}\right)^2+\dfrac{8067}{4}\ge\dfrac{8067}{4}\)
\(A_{min}=\dfrac{8067}{4}\) khi \(x=y=\dfrac{3}{2}\)
KC
1
16 tháng 10 2021
\(A=3x^2+6x+15=3\left(x^2+2x+1\right)+12\)
\(=3\left(x+1\right)^2+12\ge12\)
\(minA=12\Leftrightarrow x=-1\)
VM
20 tháng 3 2022
a, Có \(\left(x^2-9\right)^2\)≥0 ∀ x ∈ Z
|y-2| ≥0 ∀ y ∈ Z
⇒ Gía trị nhỏ nhất A=-1. Dấu ''='' xảy ra khi:\(\left(x^2-9\right)^2\)+|y-2|=0
⇒ \(x=3\) ; \(y=2\)
Vậy.....
b, Có \(x^4\) ≥ 0 ∀ x ∈ Z
3\(x^2\) ≥ 0 ∀ x ∈ Z
⇒ Giá trị nhỏ nhất của B=2. Dấu ''='' xảy ra khi: \(x^4\)+3\(x^2\)=0
⇒ \(x^2\left(x^2+3\right)\)=0
⇒ \(x^2\) =0
⇒ \(x=0\)
Vậy...
EC
2
20 tháng 3 2022
\(A=-3x^2-5\left|y-1\right|+3\le3\)
Dấu ''='' xảy ra khi x = 0 ; y = 1
20 tháng 3 2022
THAM KHẢO:
A= −3x2−5|y−1|+3 ≤ 3
Dấu ''='' xảy ra khi x = 0 ; y = 1
CM
25 tháng 9 2019
Đặt 
Khi đó hàm số trở thành y= t2- 3t+1 với t≥ 1.
Bảng biến thiên
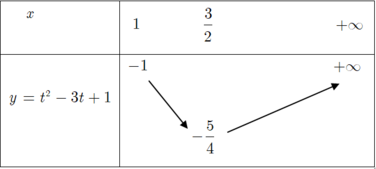
Suy ra giá trị nhỏ nhất của hàm số:
khi và chỉ khi t= 3/2 hay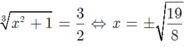 
Chọn C.
NT
2
7 tháng 7 2021
\(A=x^2-x=\left(x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}\right)-\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu "=" xảy ra khi \(x=\dfrac{1}{2}\)
Vậy \(A_{min}=-\dfrac{1}{4}\)
LT
0
NV
0
mk can gap nhe!!!!!
\(A=x^4+3x^2+2\)
Ta có:
\(x^4\ge0;3x^2\ge0\)
\(\Rightarrow A=x^4+3x^2+2\ge2\)
Vậy \(Min_A=2\Leftrightarrow x=0\)