khái niệm căn bậc hai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Căn bậc hai của một số không âm x là một số n sao cho \(n^2=x\)

Căn bậc hai của một số không âm a là một số x sao cho \(x^2=a\)
Căn bậc hai của một số là số không âm a là một số x sao cho x^2=a
bn tham khảo

Phương trình bậc nhất hai ẩn x và y có dạng ax + by = c, trong đó a, b và c là các số và a ≠ 0 hoặc b ≠ 0.
Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm. Trong mặt phẳng tọa độ, tập nghiệm của nó được biểu diễn bởi đường thẳng ax + by = c.
Chúc bạn học tốt

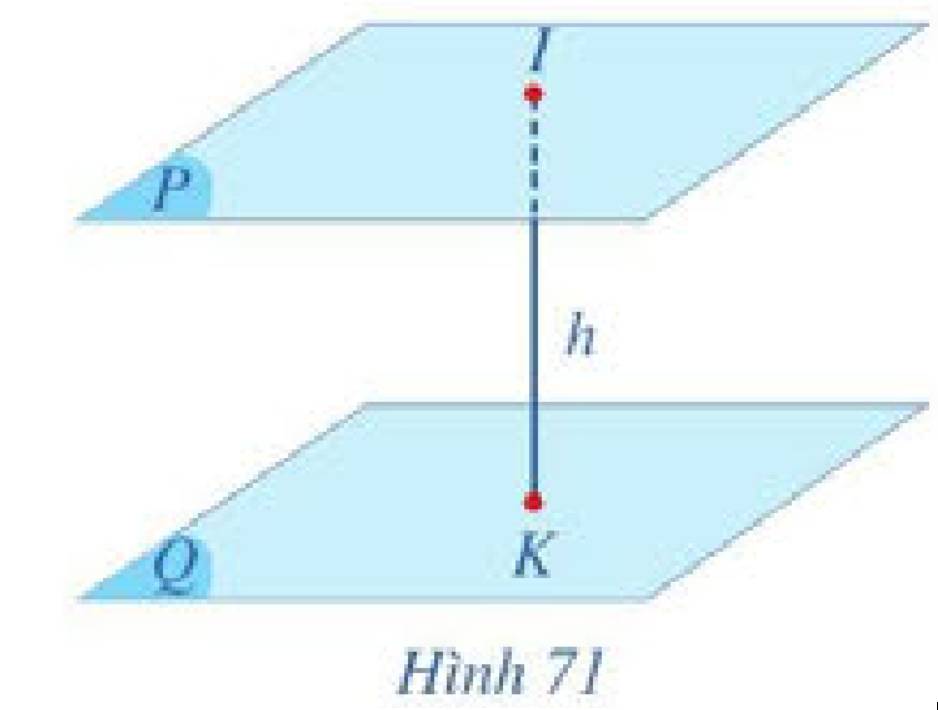
a) Khoảng cách đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song.
b)
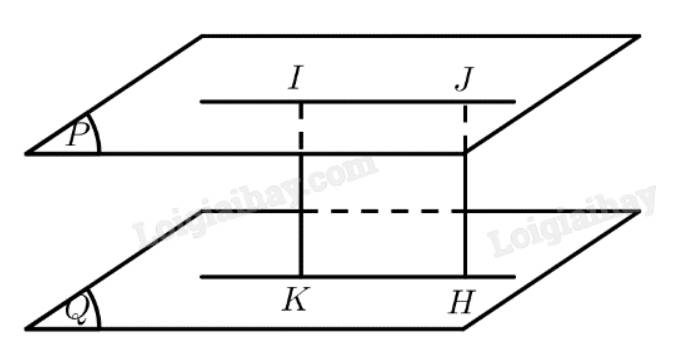
Trên mặt phẳng \(\left( P \right)\) lấy điểm \(J\) khác \(I\).
Kẻ \(JH \bot \left( Q \right)\left( {H \in \left( Q \right)} \right)\)
\( \Rightarrow HKIJ\) là hình chữ nhật \( \Rightarrow IK = JH\)
\( \Rightarrow d\left( {I,\left( Q \right)} \right) = d\left( {J,\left( Q \right)} \right)\)
Vậy khoảng cách \(IK\) từ điểm \(I\) đến mặt phẳng \(\left( Q \right)\) không phụ thuộc vào vị trí của điểm \(I\) trong mặt phẳng \(\left( P \right)\).

\(\dfrac{\left(\sqrt{3}+\sqrt{2}\right)^2+\left(\sqrt{3}-\sqrt{2}\right)^2}{\left(\sqrt{3}-\sqrt{2}\right)\left(\sqrt{3}+\sqrt{2}\right)}=\dfrac{3+2\sqrt{6}+2+3-2\sqrt{6}+2}{1}=10\)

căn bậc hai của một số a là một số x sao cho x2 = a