Question

[HÀ ANH]

Giúp mình với nhoa!!!

Answer 1

[Greninja]

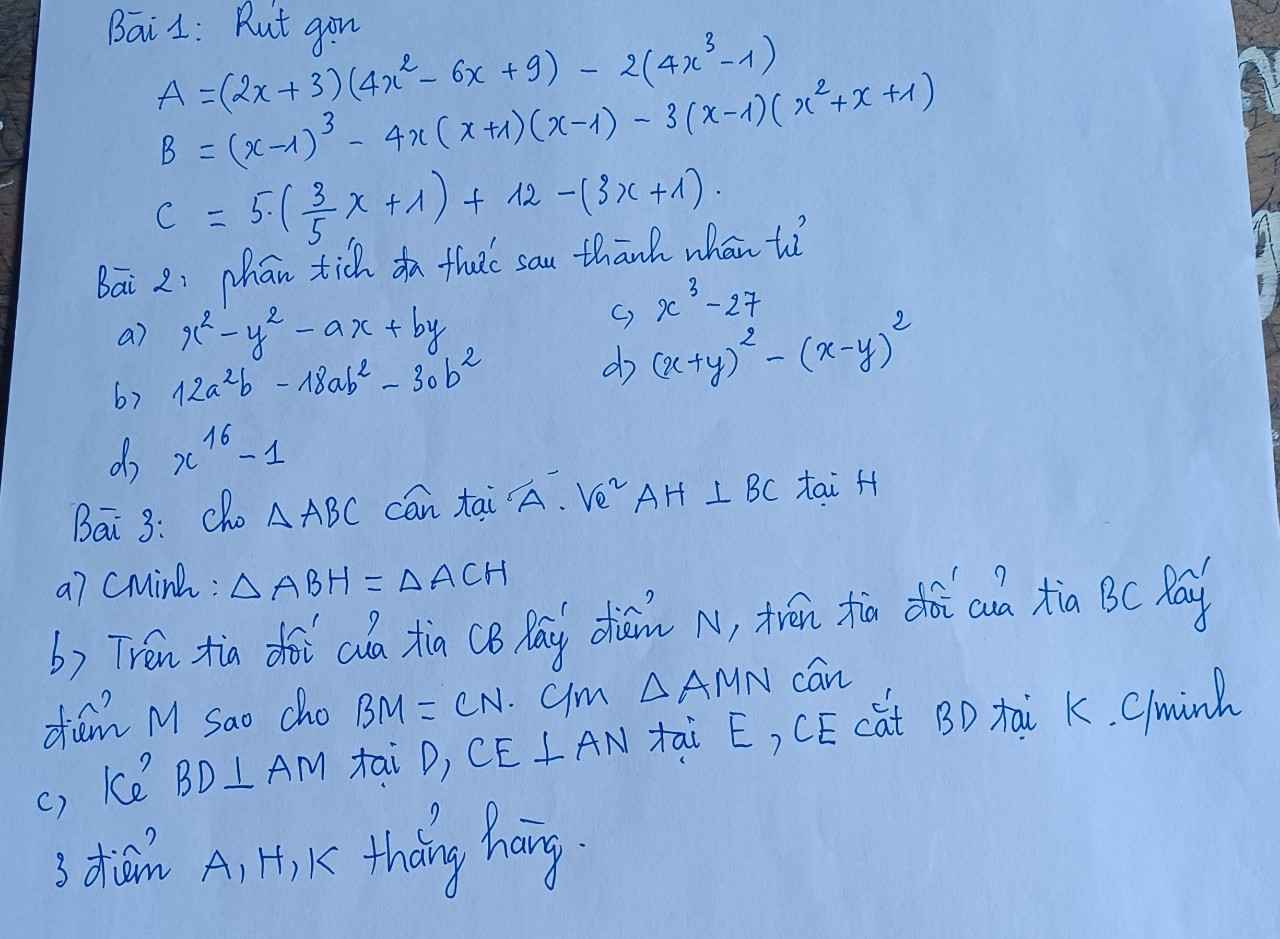
a) \(ĐKXĐ:x\ne\left\{\pm2;1\right\}\)

\(A=\left(\frac{x^3}{x^2-4}+\frac{x}{2-x}-\frac{2}{x+2}\right)\div\frac{x^2-2x+1}{x+2}\)

\(=\left(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\right)\div\frac{x^2-2x+1}{x+2}\)

\(=\left[\frac{x^3-x\left(x+2\right)-2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right]\div\frac{x^2-2x+1}{x+2}\)

\(=\frac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}\div\frac{\left(x-1\right)^2}{x+2}\)

\(=\frac{x^3-x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\div\frac{\left(x-1\right)^2}{x+2}\)

\(=\frac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}\div\frac{\left(x-1\right)^2}{x+2}\)

\(=\frac{\left(x-1\right)\left(x^2-4\right)}{x^2-4}.\frac{x+2}{\left(x-1\right)^2}\)

\(=\frac{x+2}{x-1}\)

Vậy \(A=\frac{x+2}{x-1}\)với \(x\ne\left\{\pm2;1\right\}\)

b) Ta có : \(\left|x\right|=1\Leftrightarrow\orbr{\begin{cases}x=1\left(ktm\right)\\x=-1\left(tm\right)\end{cases}}\)

với \(x=-1\Rightarrow A=\frac{-1+2}{-1-1}=\frac{-1}{2}\)

Vậy \(A=\frac{-1}{2}\)khi \(\left|x\right|=1\)

c) Ta có : \(A< 0\)

\(\Leftrightarrow\frac{x+2}{x-1}< 0\)

TH1 : \(\hept{\begin{cases}x+2< 0\\x-1>0\end{cases}\Leftrightarrow}\hept{\begin{cases}x< -2\\x>1\end{cases}}\left(ktm\right)\)

TH2 : \(\hept{\begin{cases}x+2>0\\x-1< 0\end{cases}\Leftrightarrow}\hept{\begin{cases}x>-2\\x< 1\end{cases}\left(tm\right)\Leftrightarrow}-2< x< 1\)

Vậy -2 < x < 1 để A < 0

d) \(A=\frac{x+2}{x-1}=\frac{x-1+3}{x-1}=1+\frac{3}{x-1}\)

để \(A\in Z\)thì \(\frac{3}{x-1}\in Z\)

\(\Rightarrow\left(x-1\right)\inƯ\left(3\right)=\left\{-1;1;-3;3\right\}\)

\(\Rightarrow x\in\left\{0;2;-2;4\right\}\)

kết hợp ĐKXĐ ta có : \(x\in\left\{0;4\right\}\)

Vậy \(x\in\left\{0;4\right\}\)thì \(A\in Z\)