Có bao nhiêu số nguyên dương trong tập hợp các số từ 1 đến 1000, bao gồm, là bội số của 2, 3 và 5 nhưng không phải là 8?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 5 2018
Ta có: \(BCNN\left(2;3;5\right)=30\)
\(\Rightarrow BC\left(2;3;5\right)=\left\{30;60;90;120;...\right\}\)
Mà theo đề các số này <1000
Nên \(BC\left(2;3;5\right)< 1000=\left\{30;60;90;....990\right\}\)(1)
Tập hợp (1) có tất cả: \(\frac{990-30}{30}+1=33\)(hạng tử)
Mặt khác, trong tập hợp (1) các số là\(B\left(8\right)=\left\{120;240;...;960\right\}\)(2)
Tập hợp (2) có tất cả: \(\frac{960-120}{120}+1=8\)(hạng tử)
Vậy từ 1 đến 1000 có tất cả \(33-8=25\)số vừa chia hết cho 2; 3 và 5 mà không chia hết cho 8
28 tháng 8 2023
6:
n(n+1)=6
=>n^2+n-6=0
=>(n+3)(n-2)=0
=>n=-3(loại) hoặc n=2(nhận)
4:
Ư(36)={1;-1;2;-2;3;-3;4;-4;6;-6;9;-9;12;-12;18;-18;36;-36}
=>A có 18 phần tử
1:
Ư(100)={1;-1;2;-2;4;-4;5;-5;10;-10;20;-20;25;-25;50;-50;100;-100}
3: 10;50;25
H9
HT.Phong (9A5)
CTVHS
29 tháng 8 2023
Câu 1:
\(Ư\left(100\right)=\left\{1;2;4;5;10;25;50;100\right\}\)
Câu 2:
Gọi tập hợp đó là A:
\(A=\left\{0;30;60;90;120;150;...;990\right\}\)
Câu 3:
Gọi tập hợp đó là B:
\(B=\left\{10;25;50\right\}\)
10 tháng 11 2015
c2:21 phần tử
c3:39 phần tử
c5:504 phần tử
c7:3 tập hợp
c8:12 số
c9:9 số
c10:6;8;10
17 tháng 2 2021
Cho tập hợp A = {4; 5; 6; 8; 9} và tập hợp B = {7; 8}. Số các số có hai chữ số có dạng ab, với a ∈ A và b ∈ B là ?
CM
23 tháng 11 2019
Năm số được chọn ra xếp được duy nhất dãy tăng, giả sử là
x 1 < x 2 < x 3 < x 4 < x 5
Theo giả thiết các số đó là x 1 , q x 1 , q 2 x 1 , q 3 x 1 , q 4 x 1 và q ∈ ℕ , q ≥ 2
Vì 
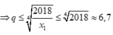
Mặt khác
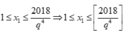
Vậy với mỗi số nguyên q thuộc tập X={ 2;3;4;5;6}
ta có 2018 q 4 cách chọn x1 các số x2, x3, x4, x5 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
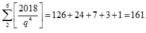
Chọn đáp án B.
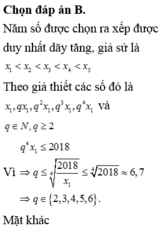
Bội của B(2,3,5)={30,900,27000,...}
Vậy có 2 số nguyên dương trong tập hợp cacs số từ 1 đến 1000 , là 30 và 900
hello