Cho đường tròn tâm O đường kính AB . Một điểm C khác A và B nằm trên đường tròn . Tiếp tuyến Cx của đường tròn tâm O cắt AB tại I . Phân giác của góc CIA cắt OC tại O' a) (O',O'C) tiếp xúc với O và tiếp xúc với AB b) Gọi D,E theo thứ tự là giao điểm thứ hai của Ca và CB với (O') C/m D,O',E thẳng hàng c) tìm vị trí của C sao cho đường tròn ngoại tiếp tam giác OCI tiếp xúc với AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 7 2018
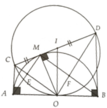
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.