cho tam giác abc có 3 góc nhọn nội tiếp đường tròn. các đường cao be và cf cắt nhau tại h
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2023
a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK
CM
19 tháng 7 2017
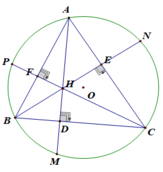
a) Xét tứ giác CEHD có:
∠(CED) = 90 0 (do BE là đường cao)
∠(HDC) = 90 0 (do AD là đường cao)
⇒ ∠(CED) + ∠(HDC) = 180 0
Mà ∠(CED) và ∠(HDC) là 2 góc đối của tứ giác CEHD nên CEHD là tứ giác nội tiếp
22 tháng 5 2022
xét tứ giác BFHD có
góc BFH + góc BDH = 180
mà nó là 2 góc đối => nội tiếp => góc FDH = góc FBE
chứng minh tương tự với tứ giác CEHD
=> góc HDE = góc HCE
Xét tứ giác BFEC có
góc BFC = góc BEF = 90
mà nó là 2 góc kề => tứ giác nội tiếp
mà góc BEC = 1/2 sđ BC = 90 => SĐ BC = 180 => BC là đường kính mà I là trung điểm BC => I là tâm đường tròn ngoại tiếp tứ giác BFEC
=> góc FIE = góc FBE + góc FCE
=> Góc FIE = góc FDH+góc HDE => góc FIE = góc FDE
mà nó là 2 góc kề => nội tiếp
=> điều phải cm
CM
25 tháng 8 2018
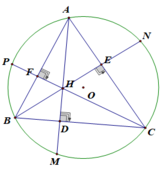
d) Tam giác ADB vuông tại D có: ∠(A1) + ∠(ABC) = 90o (1)
Tam giác BCF vuông tại F có: ∠(C1) + ∠(ABC) = 90o (2)
Từ (1)và (2) ⇒ ∠(A1) = ∠(C1)
Mặt khác, ta có: ∠( A 1 ) = ∠( C 2 ) ( 2 góc nội tiếp cùng chắn cung BM)
⇒ ∠( C 1 ) = ∠( C 2 )
⇒ CD là tia phân giác của góc HCM
Xét tam giác HCM có: CD vừa là tia phân giác vừa là đường cao (CD⊥HD)
⇒ Δ HCM cân tại C
⇒ CD cũng là trung tuyến của của HM hay H và M đối xứng với nhau qua D.
13 tháng 6 2016
Ta có hình vẽ như sau:
Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp.
CM
10 tháng 4 2017
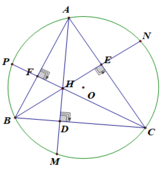
c) Xét ΔAEH và ΔADC có:
∠(AEH) = ∠(ADC) = 90 0
∠(DAC) là góc chung
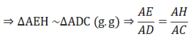
⇒ AE.AC = AD.AH
Xét Δ BEC và ΔADC có:
∠(BEC) = ∠(ADC) = 90 0
∠(ACD) là góc chung
⇒ ΔBEC ∼ ΔADC (g.g)
31 tháng 1 2023
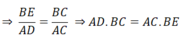
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC
Mày bị điên à???????//
Nà Ní!!!!!!!!!!!!!!!!!!!!!!!!!!!
tam giác làm sao có 3 góc nhọn dc :p