Cho mình hỏi bài 3 làm như nào với ạ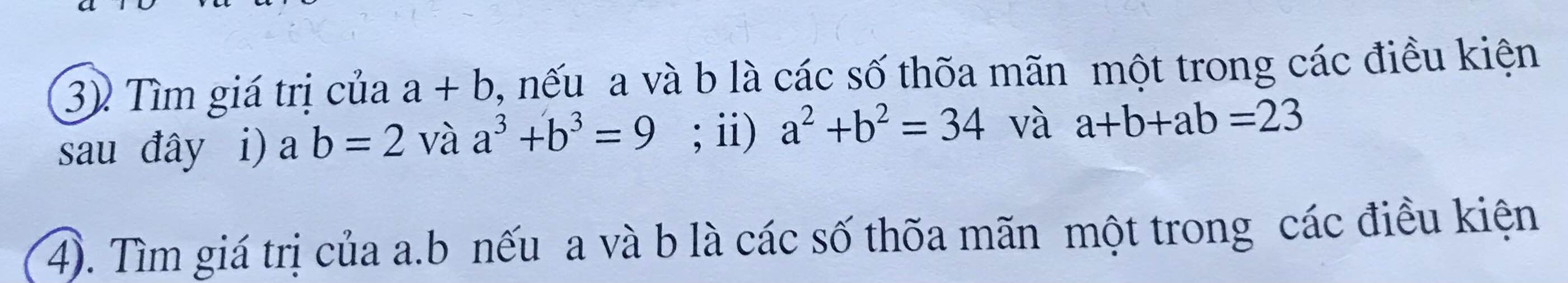
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=\(\left(3\sqrt{3}-3\sqrt{3}+2\sqrt{6}\right):3\sqrt{3}\)
\(=1-\dfrac{\sqrt{6}}{2}+\dfrac{2\sqrt{2}}{3}\)
=\(\dfrac{6}{6}-\dfrac{3\sqrt{6}}{6}+\dfrac{4\sqrt{2}}{6}\)
=\(\dfrac{6+\sqrt{6}}{6}\)

thì mình lấy giả thiết của định lí thuận làm kết luận, kết luận của định lí thuận làm giả thiết

{nhận xét về bài làm của bạn}
bạn ơi là phép tính có nhớ bạn ạ
[ lời giải ]
* ngôi nhà số 1 ( kết quả là 12) ( phép cộng )
- 5 + 7
- 6 + 6
- 4 + 8
- 9 + 3
* ngôi nhà số 2 ( kết quả là 4 ) ( phép trừ )
- 11 - 7
- 12 - 8
- 13 - 9
- 10 - 6
* ngôi nhà sồ 3 (kết quả là 5 ) ( phép trừ )
- 13 - 8
- 12 - 7
- 11 - 6
- 10 - 5
[giải thích (hoặc là hướng dẫn) cách làm]
- bạn chỉ cần tạo ra 1 phép tính có nhớ trong phạm vi 20
- mỗi ngôi nhà có kết quả và mẫu phép tính
- bạn cần đọc và hiểu mẫu đề bài cho rồi tự làm
Đáp án : sai. 6-2 không phải là phép tính có nhớ còn nhiều lỗi lắm

Về lý thuyết thì có thể tính toán chính xác được điểm rơi mà ko cần đoán, nhưng thực tế thì dạng này thường tách A để xuất hiện \(a+2b+3c\) và phần còn lại sẽ tự ghép:
\(4A=4a+4b+4c+\dfrac{12}{a}+\dfrac{18}{b}+\dfrac{16}{c}\)
\(\Rightarrow4A=a+2b+3c+\left(3a+\dfrac{12}{a}\right)+\left(2b+\dfrac{18}{b}\right)+\left(c+\dfrac{16}{c}\right)\)
\(\Rightarrow4A\ge20+2\sqrt{\dfrac{36a}{a}}+2\sqrt{\dfrac{36b}{b}}+2\sqrt{\dfrac{16c}{c}}=...\)

\(\frac{3}{5}\div x=\frac{1}{3}\)
\(x=\frac{3}{5}\div\frac{1}{3}=\frac{9}{5}\)

\(\left[\left(20-2^3.4\right)+\left(3^2.4.16\right)\right]:5\)
\(=\left[\left(-12\right)+576\right]:5\)
\(=564:5=112,8\)
PP/ss: Có thể tính sai ạ ((:
\(\left[\left(20-2^3.4\right)+\left(3^2.4.16\right)\right]:5\)
\(=\left[-12+\left(3^2.4.16\right)\right]:5\)
\(=\left(-12+576\right):5\)
\(=564:5\)
\(=\frac{564}{5}\)
 cho mình hỏi bài 5 này làm như nào ạ, mình làm như thế đã đúng chưa
cho mình hỏi bài 5 này làm như nào ạ, mình làm như thế đã đúng chưa


i)\(\left\{{}\begin{matrix}ab=2\\a^3+b^3=9\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}ab=2\\\left(a+b\right)^3-3ab\left(a+b\right)=9\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^3-6\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b\right)^3-3\left(a+b\right)^2+3\left(a+b\right)^2-9\left(a+b\right)+3\left(a+b\right)-9=0\)
\(\Leftrightarrow\left(a+b-3\right)\left[\left(a+b\right)^2+3\left(a+b\right)+3\right]=0\)
\(\Leftrightarrow a+b=3\)( \(\left(a+b\right)^2+3\left(a+b\right)+3>0;\forall a,b\)
ii) \(\left\{{}\begin{matrix}a+b+ab=23\\a^2+b^2=34\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}ab=23-\left(a+b\right)\\\left(a+b\right)^2-2ab=34\end{matrix}\right.\)
\(\Rightarrow\left(a+b\right)^2-2\left[23-\left(a+b\right)\right]=34\)
\(\Leftrightarrow\left(a+b\right)^2+2\left(a+b\right)-80=0\)
\(\Leftrightarrow\left(a+b-8\right)\left(a+b+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=8\\a+b=-10\end{matrix}\right.\)