Giải phương trình sau:
(x-1)3 + x3 + (x+1)3 = (x+2)3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 2 2017
a) Biến đổi về dạng (x - 3)(x + 2) = 0. Tìm được x ∈ { - 2 ; 3 }
b) Thu gọn về dạng -2x + 3 = 0. Tìm được x = 3 2
24 tháng 8 2023
b: 4(x+1)^2-9(x-1)^2=0
=>(2x+2)^2-(3x-3)^2=0
=>(2x+2-3x+3)(2x+2+3x-3)=0
=>(-x+5)(5x-1)=0
=>x=1/5 hoặc x=5
c: (x-1)^3+x^3+(x+1)^3=(x+2)^3
=>x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8
=>3x^3+6x-x^3-6x^2-12x-8=0
=>2x^3-6x^2-6x-8=0
=>x^3-3x^2-3x-4=0
=>x^3-4x^2+x^2-4x+x-4=0
=>(x-4)(x^2+x+1)=0
=>x-4=0
=>x=4
MN
17 tháng 2 2020
a) \(x^3+2\left(x-1\right)^2-2\left(x-1\right)\left(x+1\right)=x^3+x-4-\left(x-7\right)\).
\(\Leftrightarrow x^3+2\left(x^2-2x+1\right)-2\left(x^2-1\right)=x^3+x-4-x+7\)
\(\Leftrightarrow x^3+2x^2-4x+2-2x^2+2=x^3+3\)
\(\Leftrightarrow x^3-4x+4=x^3+3\)
\(\Leftrightarrow4x-1=0\)
\(\Leftrightarrow x=\frac{1}{4}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{4}\right\}\)
b) \(2\left(x-3\right)+1=2\left(x+1\right)-9\)
\(\Leftrightarrow2x-6+1=2x+2-9\)
\(\Leftrightarrow2x-5=2x-7\)
\(\Leftrightarrow2=0\)(ktm)
Vậy tập nghiệm của phương trình là \(S=\varnothing\)
c) \(3\left(x+1\right)\left(x-1\right)-5=3x^2+2\)
\(\Leftrightarrow3\left(x^2-1\right)-5=3x^2+2\)
\(\Leftrightarrow3x^2-3-5=3x^2+2\)
\(\Leftrightarrow3x^2-8=3x^2+2\)
\(\Leftrightarrow0=10\)(ktm)
Vậy tập nghiệm của phương trình là \(S=\varnothing\)
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
PT
1
CM
27 tháng 9 2019
Ta có:
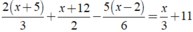
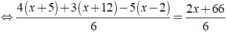
⇔ 4x + 20 + 3x + 36 - 5x + 10 = 2x + 66
⇔ 0x = 0
⇒ Phương trình đã cho vô số nghiệm.
Vậy phương trình đã cho vô số nghiệm.
CM
17 tháng 12 2017
a) Triển khai hằng đẳng thức và rút gọn được 8x + 12 = 0
Từ đó tìm được x = - 3 2
b) Sử dụng hằng đẳng thức, biến đổi phương trình về dạng: (x - 3)(2 x 2 - 4x) = 0
Sưe dụng phương pháp giải PT tích tìm được x ∈ {0; 2; 3}
c) Quy đồng khử mẫu ta được 48x - 16 = 0
Từ đó tìm được x = 1 3
d) Quy đồng khử mẫu ta được 3x + 6 = 2x + 63
Từ đó tìm được x = 57.
22 tháng 7 2021
b) 5x(x-2000)-x+2000=0
\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)
\(\left(x-1\right)^3+x^3+\left(x+1\right)^3=\left(x+2\right)^3\)
\(\Leftrightarrow\)\(x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8\)
\(\Leftrightarrow\)\(3x^3+6x=x^3+6x^2+12x+8\)
\(\Leftrightarrow\)\(2x^3-6x^2-6x-8=0\)
\(\Leftrightarrow\)\(x^3-3x^2-3x-4=0\)
\(\Leftrightarrow\)\(x^3-4x^2+x^2-4x+x-4=0\)
\(\Leftrightarrow\)\(\left(x-4\right)\left(x^2+x+1\right)=0\)
\(\Leftrightarrow\)\(x-4=0\) (vì x2 + x + 1 = (x + 0,5)2 + 0,75 > 0)
\(\Leftrightarrow\)\(x=4\)
Vậy...