Một quặng X chứa 64% Fe2O3 và quặng Y chứa 69,6% Fe3O4. Trộn a tấn quặng X với b tấn quặng Y thu được một loại quặng Z.Biết từ một tấn quặng Z có thể điều chế được 481,25kg gang chứa 4% cacbon( gang là hợp chất gồm Fe và C)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2)
Giả sử có 1 mol A
PTHH: 4A --to--> 4B + C + 2D
1------->1-->0,25->0,5
=> nkhí sau pư = 1 + 0,25 + 0,5 = 1,75 (mol)
BTKL: mA = mB + mC + mD
Có \(\overline{M}=\dfrac{m_B+m_C+m_D}{1,75}=18.2=36\)
=> mA = 63 (g)
=> \(M_A=\dfrac{63}{1}=63\left(g/mol\right)\)
câu 1) đề có nói rõ điều chế 481,25kg gang từ bao nhiêu Z không vậy bn :) ?

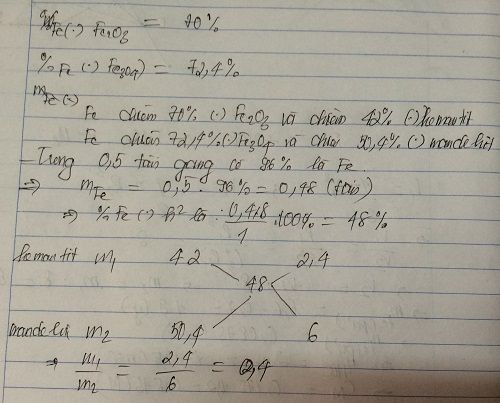
đề sai sai nha !
X là quặng hematit chứa 60% Fe2O3, Y là quặng manhetit chứa 69,6% Fe3O4. Cần trộn X, Y theo tỉ lệ khối lượng như thế nào để được quặng Z mà từ 1 tấn quặng Z có thể điều chế được 0,5 tấn gang chứa 96% sắt?OK!

trong gang:nFe =3/350
BT ng tu ngto:2nFe2O3+3nFe3O4=3/350
=>2*0.6*m1/160+3*0.696*m2/232=3/350
m1+m2=1
=>m1=2/7;m2=5/7
=>m1:m2=2/5

Đặt mA = a (tấn); mB = b (tấn)
Giả sử a + b = 1 (tấn) (1)
\(m_{Fe_2O_3\left(A\right)}=a.60\%=0,6a\left(tấn\right)=6.10^5a\left(g\right)\)
=> \(n_{Fe_2O_3\left(A\right)}=\dfrac{6.10^5a}{160}=3750a\left(mol\right)\Rightarrow n_{Fe\left(A\right)}=7500a\left(mol\right)\)
\(m_{Fe_3O_4\left(B\right)}=b.69,6\%=0,696b\left(tấn\right)=696.10^3b\left(g\right)\)
=> \(n_{Fe_3O_4\left(B\right)}=\dfrac{696.10^3b}{232}=3000b\left(mol\right)\Rightarrow n_{Fe\left(B\right)}=9000b\left(mol\right)\)
\(n_{Fe\left(tổng\right)}=\dfrac{0,48.10^6}{56}=\dfrac{60000}{7}\left(mol\right)\)
=> \(7500a+9000b=\dfrac{60000}{7}\) (2)
(1)(2) => \(a=\dfrac{2}{7}\left(tấn\right);b=\dfrac{5}{7}\left(tấn\right)\)
=> \(\dfrac{a}{b}=\dfrac{2}{5}\)

Đặt mA = a (tấn); mB = b (tấn)
Giả sử a + b = 1 (tấn) (1)
\(m_{Fe_2O_3\left(A\right)}=a.60\%=0,6a\left(tấn\right)=6.10^5a\left(g\right)\)
=> \(n_{Fe_2O_3\left(A\right)}=\dfrac{6.10^5a}{160}=3750a\left(mol\right)\Rightarrow n_{Fe\left(A\right)}=7500a\left(mol\right)\)
\(m_{Fe_3O_4\left(B\right)}=b.69,6\%=0,696b\left(tấn\right)=696.10^3b\left(g\right)\)
=> \(n_{Fe_3O_4\left(B\right)}=\dfrac{696.10^3b}{232}=3000b\left(mol\right)\Rightarrow n_{Fe\left(B\right)}=9000b\left(mol\right)\)
\(n_{Fe\left(tổng\right)}=\dfrac{0,48.10^6}{56}=\dfrac{60000}{7}\left(mol\right)\)
=> \(7500a+9000b=\dfrac{60000}{7}\) (2)
(1)(2) => \(a=\dfrac{2}{7}\left(tấn\right);b=\dfrac{5}{7}\left(tấn\right)\)
=> \(\dfrac{a}{b}=\dfrac{2}{5}\)



%Fe = 100% -4% = 96%
$m_{Fe} = 481,25.96% = 462(gam)$
$n_{Fe} = 462 : 56 = 8,25(kmol)$
Ta có : $a + b = 1(1)$
$m_{Fe_2O_3} = 1000a.64\% = 640a(kg)$
$\to n_{Fe_2O_3} = 640a : 160 = 4a(kmol)$
$m_{Fe_3O_4} = 1000b.69,6\% = 696b(kg)$
$\to n_{Fe_3O_4} = 696b : 232 = 3b(kmol)$
Bảo toàn nguyên tố với Fe :
$4a.2 + 3b.3 = 8,25(2)$
Từ (1)(2) suy ra a = 0,75(tấn) ; b = 0,25(tấn)