xy4.(91x4y3−2x3)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Nếu y dương hay âm thì y2, y4 luôn dương nên ta không cần xét.
- Nếu x dương thì đơn thức A dương nhưng B âm.
- Nếu x âm thì đơn thức B dương nhưng A âm.
-> Vậy hai đơn thức không thể cùng có giá trị dương.

Vì đơn thức -2/3 x(a + 2)yb đồng dạng với đơn thức -1/3 x4y3 nên ta có:
a + 2 = 4 và b = 3. Từ đây suy ra a = 2, b = 3. Chọn D

Thu gọn đa thức
B(x) = x3y4 - 5y8 + x3y4 + xy4 + x3 - y2 - xy4 + 5y8
= 3x3y4 + x3 - y2
Bậc của đa thức là 7. Chọn B

x3y4 - 5y8 + x3y4 + xy4 + x3 - y2 - xy4 + 5y8
= (x3y4 + x3y4) + (xy4 – xy4) + (-5y8 + 5y8) + x3 – y2
= (1+ 1)x3y4 + (1 – 1).xy4 + ( - 5+ 5)y8 + x3 – y2
= 2x3y4 + x3 - y2.
Đa thức có bậc là 7.

a: \(M=6x^6y+x^4y^3-y^7-4x^4y^3+10-5x^6y+2y^7-2.5\)
\(=x^6y-3x^4y^3+y^7+7.5\)
Bậc là 7
b: Thay x=-1 và y=1 vào M, ta được:
\(M=\left(-1\right)^6\cdot1-3\cdot\left(-1\right)^4\cdot1^3+1^7+7.5\)
\(=1-3+1+7.5\)
=6,5

a: \(M=3x^5y^3-3x^5y^3-4x^4y^3+2x^4y^3+7xy^2=-2x^4y^3+7xy^2\)
b: \(P\left(x\right)=2x^3-2x+x^2-x^3+3x+2=x^3+x^2+x+2\)
c: \(M\left(x\right)=-3x^4y^3+10+xy\)
\(a)M=3x^5y^3-4x^4y^3+2x^4y^3+7xy^2-3x^5y^3\)
\(M=\left(3x^5y^3-3x^5y^3\right)+\left(-4x^4y^3+2x^4y^3\right)+7xy^2\)
\(M=-2x^4y^3+7xy^2\)
\(\text{Bậc là:}7\)
\(b)P\left(x\right)=2x^3-2x+x^2-x^3+3x+2\)
\(P\left(x\right)=\left(2x^3-x^3\right)+\left(-2x+3x\right)+x^2+2\)
\(P\left(x\right)=x^3+x+x^2+2\)
\(P\left(x\right)=x^3+x^2+x+2\)
\(\text{Bậc là:}3\)
\(M=\left(6x^6y-6x^6y\right)+\left(x^4y^3-4x^4y^3\right)+10+xy\)
\(M=-3x^4y^3+10+xy\)
\(\text{Bậc là:}7\)

a: \(3xy^3\cdot x^4y^2=3x^5y^2\)
b: \(\dfrac{4}{5}x^4y^2\cdot\left(-5\right)xy^3=-4x^5y^5\)
c: \(\dfrac{1}{7}x^2y\cdot\dfrac{2}{5}xy^4=\dfrac{2}{35}x^3y^5\)
a. 3xy3 . 2x4y
= 6x5y4
b. \(\dfrac{12}{15}x^4y^2.\left(-5\right)xy^3\)
= -4x5y5
c. \(\dfrac{-1}{7}x^2y.\dfrac{-2}{5}xy^4\)
= \(\dfrac{2}{35}x^3y^5\)

Đặt và thực hiện phép tính ta có :
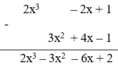
Vậy chọn đa thức thứ hai.