Cho tam giác ABC cân tại A.Gọi G là trọng tâm,O là giao điểm của 2 đường trung trực cạnh AB,AC.chứng minh rằng :
a,tam giác BOC cân
b, ba điểm A,O,G thẳng hàng
Giúp mình nhanh lên .cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2019
a)G là trọng tâm tam giác ABC (giả thiết) => AG là trung tuyến tam giác ABC => A, G, M thẳng hàng (*)
=> AM trùng AG => 2GM = GA (tc trọng tâm) (b)
Từ (a) có: OM // AH => góc HAM = góc AMO (so le trong) (c)
Từ (a), (b), (c) => tam giác AGH và MGO đồng dạng
=> góc AGH = góc MGO (**)
Từ (*) và (**) => A, G, O thẳng hàng.
b) Bí !!!
17 tháng 9 2023
a)
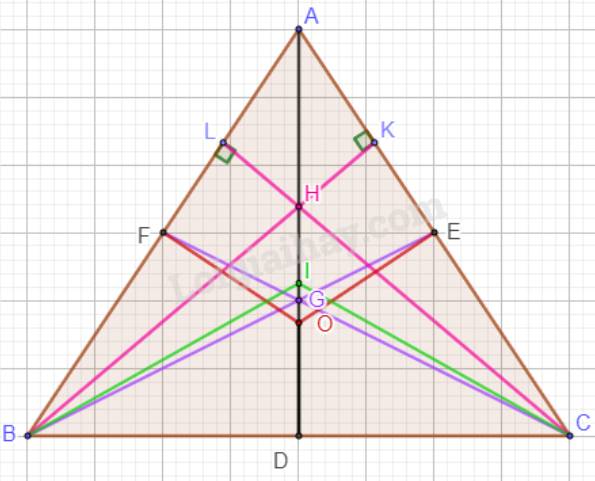
Trong tam giác ABC cân tại A có AD là đường trung tuyến.
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân);
AD chung;
BD = DC (D là trung điểm của BC).
Vậy \(\Delta ABD = \Delta ACD\)(c.c.c.). Suy ra: \(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (vì ba điểm B, D, C thẳng hàng); \(\widehat {BAD} = \widehat {CAD}\).
Vậy AD là đường cao của tam giác và đường phân giác của góc A.
Suy ra: AD là đường trung trực của tam giác ABC.
Vậy AD là đường trung tuyến, đường cao, đường phân giác, đường trung trực của tam giác ABC.
Mà G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực nên A, G, H, I, O cùng nằm trên một đường thẳng.
Vậy nếu tam giác ABC cân tại A thì các điểm A, G, H, I, O cùng nằm trên một đường thẳng.
b)
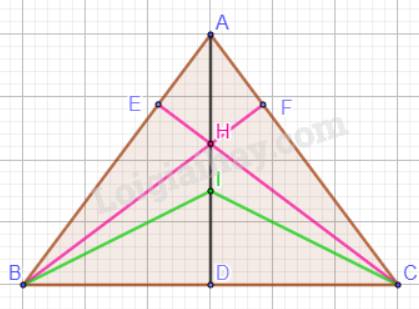
Ta có: \(AD \bot BC\).
H là trực tâm của tam giác ABC nên A, H, D thẳng hàng.
Mà A, H, I thẳng hàng nên A, H, I, K thẳng hàng.
Suy ra: AD là tia phân giác của góc BAC (Vì AI là tia phân giác của góc BAC).
Nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác BAD và tam giác CAD có:
\(\widehat {BAD} = \widehat {CAD}\);
AD chung;
\(\widehat {ADB} = \widehat {ADC}\) (\(AD \bot BC\)).
\(\Rightarrow \Delta ABD = \Delta ACD\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng).
Do đó, tam giác ABC cân tại A
Vậy nếu các điểm A, H, I cùng nằm trên một đường thẳng thì tam giác ABC cân tại A.
9 tháng 4 2018
Kẻ đường phân giác của ˆAA^ và ˆCC^ cắt nhau tại I, AI cắt BC tại M.
∆ABC cân tại A.
Đường phân giác AM cũng là đường trung tuyến (tính chất tam giác cân)
G là trọng tâm của ∆ABC
⇒⇒ G ∈ AM
Vậy A, I, G thẳng hàng.
Bạn k cho mk nha !!!
CM
27 tháng 12 2019
ΔABC cân tại A
⇒ phân giác AI đồng thời là trung tuyến
⇒ AI đi qua trọng tâm G của ΔABC
Vậy A, I, G thẳng hàng.
a.tam giác ABC có O là giao điểm của 2 đường trung trực cạnh AB,AC
=>OA=OB và OA=OC
=>OB=OC=>tam giác BOC cân tại O
b.vì O là giao điểm của hai đường trung trực của tam giácABC=>AO là đương trung trực con lại của tam giác ABC
mà tam giác ABC cân tại A
=>AO đồng thời là đường trung tuyến ứng với cạnh BC của tam giác ABC mà G là trọng tâm của tam giác ABC(gt)
=>\(G\in AO\)=> ba điểm A,O,G thẳng hàng