Cho tam giác ABC cân tại A .Kẻ BH vuông góc AC(H thuộc AC), CK vuông góc AB .Chứng minh AH = AK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ΔABC cân tại A
=> Góc B = góc C
=> AB = AC
Xét 2 ΔKBC và ΔHCB có
Góc B = góc C
BC chung
Góc BKC = góc BHC = 90o
=> ΔKBC = ΔHCB (c - g - c)
=> BK = HC
Mà AB = AC (cmt)
=> AK = AH (dpcm)

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{BAH}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)

A B C K H
Xét tam giác AKC và tam giác AHB có:
AB = AC ( do tam giác ABC cân tại A ) ( gt )
Góc A là góc chung
Góc AKC = góc AHB ( = 90 độ ) ( gt )
=> Tam giác AKC = tam giác AHB ( ch.gn )
=> AK = AH ( 2 cạnh tương ứng )

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC
 hãy cho mk 1 L-I-K-E
hãy cho mk 1 L-I-K-E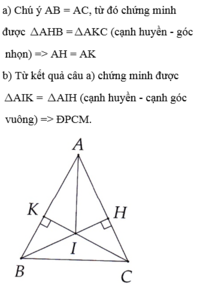
Bạn tự vẽ hình nhé !
Xét tam giác vuông ABH và tam giác vuông ACK có:
AB = AC ( tam giác ABC cân tại A )
 chung
Vậy tam giác ABH = tam giác ACK ( ch.gn )
=> AH = AK ( 2 cạnh tương ứng )
Bạn vẽ cả hình giúp mình với