Cho tam giác ABC, vẽ phân giác AD (D thuộc BC). Chứng minh: AD2 < AB . AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2024
a: Ta có: \(\widehat{MAD}=\widehat{BAD}\)(AD là tia phân giác của góc BAC)
\(\widehat{BAD}=\widehat{MDA}\)(hai góc so le trong, AB//DM)
Do đó: \(\widehat{MAD}=\widehat{MDA}\)
=>ΔMAD cân tại M
b: Xét ΔMND và ΔBDN có
\(\widehat{MND}=\widehat{BDN}\)(hai góc so le trong, NM//BD)
ND chung
\(\widehat{MDN}=\widehat{BND}\)(hai góc so le trong, MD//BN)
Do đó: ΔMND=ΔBDN
c: Ta có: ΔMND=ΔBDN
=>MD=BN
mà MD=MA
nên MA=BN
D
5 tháng 4 2016
a)
ta có : AB<AC
suy ra ACB<ABC
ABH=90-60=30
b)
DAC=DAB=90-(A/2)=90-30=60
ABI=90-30=60
xét 2 tam giác vuông AIB và BHA có
AB(chung)
ta có:
BAH=ABD=60(cmt)
suy ra AIB=BHA(CH-GN)
c)
theo câu a, ta có tam giác AIB=BHA(CH-GN)
suy ra ABI=BAC=60 độ
BEA=180-60-60=60 độ
ta có: ABE=BEA=EAB=60 suy ra tam giác ABE đều
5 tháng 4 2016
a,Ta có :
AB<AC (gt)
=> C<B
=> góc ABC < góc ACB
Tính góc ABH
Ta có : A+H+B=180 ( tổng 3 góc trong 1 tam giác )
60+90+B=180 ( góc H =90 vì vuông góc )
150+B=180
B=180-150
B=30
=>ABH=30
b,Xét 2 tg AIB= tg BHA vuông tại I và H
Có : I là góc chung
=> tg AIB= tg BHA(gcg)
c,ko bt lm
d,ko bt luôn
CM
16 tháng 12 2018
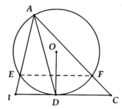
a, HS tự chứng minh
b, ∆ADE:∆ACD (g.g)
=> A D 2 = A E . A C
c, Tương tự: ∆ADF:∆ABD => A D 2 = A B . A F => ĐPCM
31 tháng 12 2023
a: Xét ΔADB và ΔADC có
AB=AC
AD chung
BD=CD
Do đó: ΔADB=ΔADC
b: Ta có: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
c: Xét ΔADM vuông tại M và ΔADN vuông tại N có
AD chung
\(\widehat{DAM}=\widehat{DAN}\)
Do đó: ΔADM=ΔADN
=>AM=AN
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC