Một người đo chiều cao của tháp được đặt cách xa người đó 1500m bằng cách cong 5 ngón tay lại để che hết cái tháp. Biết cánh tay người đó dài 1 m và ngón tay cao 5cm. Em hãy tính xem tháp cao bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 10 2017
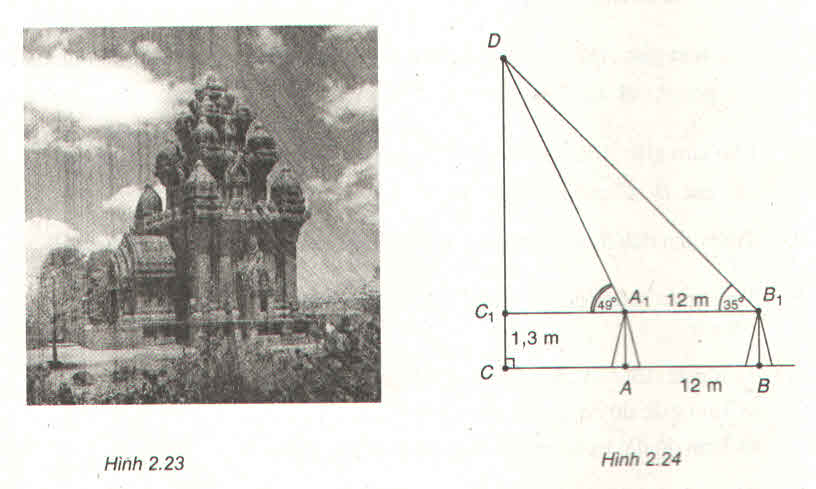
Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
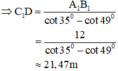
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
Chiều của ngọn tháp là:
\(\dfrac{99}{4}:2=\dfrac{99}{8}\left(m\right)\)
Đáp số: \(\dfrac{99}{8}m\)
24 tháng 8 2023
Chiều cao của ngọn tháp là:
\(\dfrac{99}{4}:2=\dfrac{99}{8}\left(m\right)\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(\widehat {D{A_1}{C_1}} = \widehat {{A_1}D{B_1}} + \widehat {D{B_1}{A_1}} \Rightarrow \widehat {{A_1}D{B_1}} = {49^ \circ } - {35^ \circ } = {14^ \circ }\)
Áp dụng định lí sin trong tam giác \({A_1}D{B_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {B_1}}} = \frac{{{A_1}{B_1}}}{{\sin D}} \Leftrightarrow \frac{{{A_1}D}}{{\sin {{35}^ \circ }}} = \frac{{12}}{{\sin {{14}^ \circ }}}\\ \Rightarrow {A_1}D = \sin {35^ \circ }.\frac{{12}}{{\sin {{14}^ \circ }}} \approx 28,45\end{array}\)
Áp dụng định lí sin trong tam giác \({A_1}D{C_1}\) , ta có:
\(\begin{array}{l}\frac{{{A_1}D}}{{\sin {C_1}}} = \frac{{{C_1}D}}{{\sin {A_1}}} \Leftrightarrow \frac{{28,45}}{{\sin {{90}^ \circ }}} = \frac{{{C_1}D}}{{\sin {{49}^ \circ }}}\\ \Rightarrow {C_1}D = \sin {49^ \circ }.\frac{{28,45}}{{\sin {{90}^ \circ }}} \approx 21,47\end{array}\)
Do đó, chiều cao CD của tháp là: \(21,47 + 1,2 = 22,67\;(m)\)
AT
30 tháng 3 2017
Ta có: Chiều cao của tháp DC = DC1 + C1C = 1,3 + DC1
=> DC = 1,3 +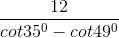 
=> DC ≈ 22,8m
30 tháng 3 2017
cãi đi bé Bài 11 trang 60 sgk hình học 10 - loigiaihay.com