
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=3.6\left(cm\right)\)
CH=BC-BH=6,4(cm)


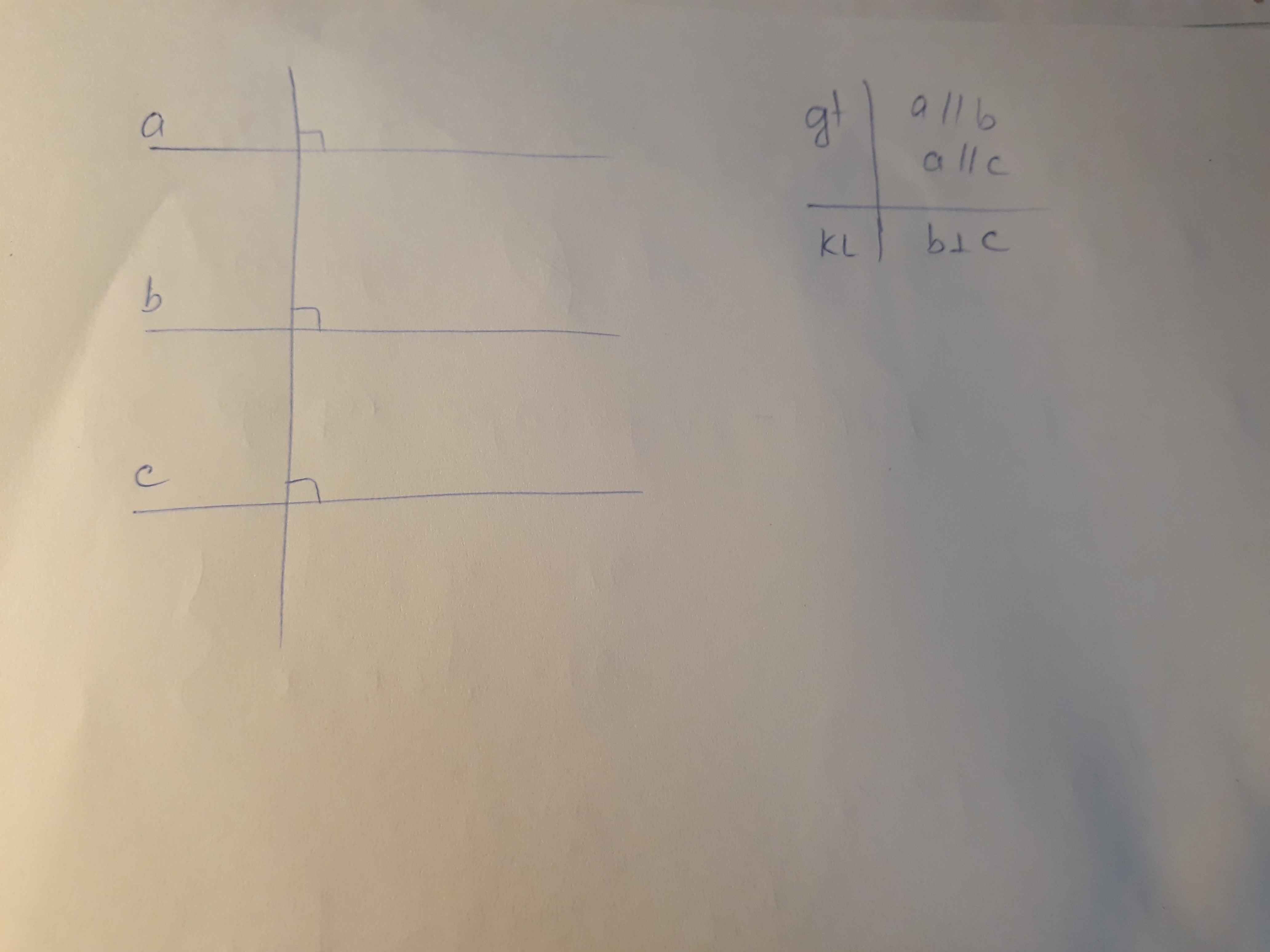
Nếu 1 đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
GT: a//b
a vuông góc với c
=> b vuông góc với c

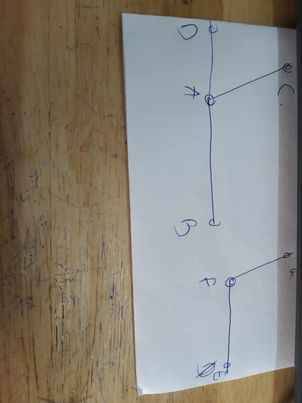
| GT | \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau |
| KL | \(\widehat{CAB}=\widehat{GFE}\) |
Vì \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{CAB}=180^0\)
=>\(\widehat{CAB}=180^0-\widehat{CAD}\left(1\right)\)
Vì \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{GFE}=180^0\)
=>\(\widehat{GFE}=180^0-\widehat{CAD}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{CAB}=\widehat{GFE}\)


a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM



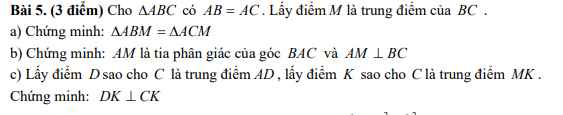
M N P I Q K E F
GT : Tam giác MNP ; MN = MP ; trung tuyến MI
KL : a) MI \(\perp\)NP
b) Cho \(IQ\perp MN;IK\perp MP\); CM : IQ = IK ; IM trung trực QK
c) Cho QE = QI ; KI = KF ; cm : Tam giác MEF cân
d) FE//NP
a) Xét tam giác MNI và MPI có :
\(\hept{\begin{cases}MN=MP\\MI\text{ chung }\\NI=IP\end{cases}}\Rightarrow\Delta MNI=\Delta MPI\Rightarrow\widehat{MIP}=\widehat{MIN}\left(1\right)\)
mà \(\widehat{MIP}+\widehat{MIN}=180^{\text{o}}\left(2\right)\)
Từ (1)(2) => \(\widehat{MIP}=\widehat{MIN}=90^{\text{o}}\)
=> MI \(\perp NP\)
b) Xét tam giác IQN và tam giác IKP có :
\(\hept{\begin{cases}\widehat{KIP}=\widehat{QIN}\left(\text{vì}\widehat{QNI}=\widehat{KPI};\widehat{NQI}=\widehat{KPI}\right)\\NI=IP\\\widehat{QNI}=\widehat{KPI}\end{cases}}\)
=> \(\Delta IQN=\Delta IKP\Rightarrow IQ=IK\)(0)
Gọi H là giao điểm của QK và MI
Tương tự ta có \(\Delta MQH=\Delta MKH\)
=> MQ = MK
=> Tam giác MQK cân tại Q
Khi đó \(\widehat{MQK}=\frac{180^o-\widehat{QMK}}{2}\)(1)
Tương tự với tam giác MNP cân tại M
=> \(\widehat{QNP}=\frac{180^{\text{o}}-\widehat{NMP}}{2}\)(2)
=> \(\widehat{MQK}=\widehat{QNP}\Rightarrow QK//NP\Rightarrow\widehat{NHK}=\widehat{MIP}=90^{\text{o}}\)(3)
Từ (0) và (3) => IM là đường trung trực của QK