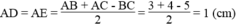Cho tam giác ABC nội tiếp đường tròn (O) đường kính AC (BA<BC). TRên đoạn đường AC lấy điểm I bất kì, I khác A;O;C. Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là D. kẻ CH vuông góc với BD \((H\in BD)\), DK vuông góc với AC \(\left(K\in AC\right)\)
a) C/m tứ giác DHKC là tứ giác nội tiếp
b) Cho độ dài đạon thẳng AC là 4cm, C/m rằng \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)