Cho O là một điểm nằm trong hình chữ nhật ABCD.
Nối O với 4 đỉnh A, B, C, D chia hình chữ nhật thành 4 tam
giác (như hình vẽ). Tính diện tích tam giác OBC, biết diện tích
các tam giác OAB, OAD, OCD lần lượt là 14cm2; 10cm2; 18cm2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2018
- Giải
- Diện tích tam giác OBC là:
- (14+10+18) : 2+1=22 cm2
DL
29 tháng 12 2018
Trong hình chữ nhật ABCD gọi chiều cao ứng với các tam giác OAB,OBC,ODC,OAD lần lượt là \(h_1,h_2,h_3,h_4\)
Với mọi \(O\in ABCD\)có \(S_{OAB}+S_{ODC}=\frac{AB.h_1}{2}+\frac{CD.h_3}{2}=\frac{AB\left(h_1+h_2\right)}{2}=\frac{1}{2}S_{ABCD}\)
Vì AB = CD
Tương tự ta có \(S_{ADO}+S_{OBC}=\frac{AD\left(h_2+h_4\right)}{AB}=\frac{AD.BC}{2}=\frac{1}{2}S_{ABCD}\)
Vậy \(S_{OAB}+S_{ODC}=S_{ADO}+S_{OBC}\)
\(14+18=10+S_{OBC}\)
\(\Rightarrow....\)
16 tháng 12 2021
Vì O là giao 2 đường trung trực của AB và BC (t/c trục đx) nên \(OA=OB;OB=OC\Rightarrow OA=OB=OC\)
Kẻ \(BH\bot AC\)
\(\Rightarrow\dfrac{S_{OAB}}{S_{OBC}}=\dfrac{\dfrac{1}{2}BH\cdot OA}{\dfrac{1}{2}BH\cdot OC}=\dfrac{OA}{OC}=1\left(OA=OC\right)\\ \Rightarrow S_{OAB}=S_{OBC}\)
31 tháng 3 2019
diện tích hình tam giác obc là : (10 + 14 +18 ) : 2 +1 = 22 (cm2)
Đáp số : 22 cm2
MH
11 tháng 4 2022
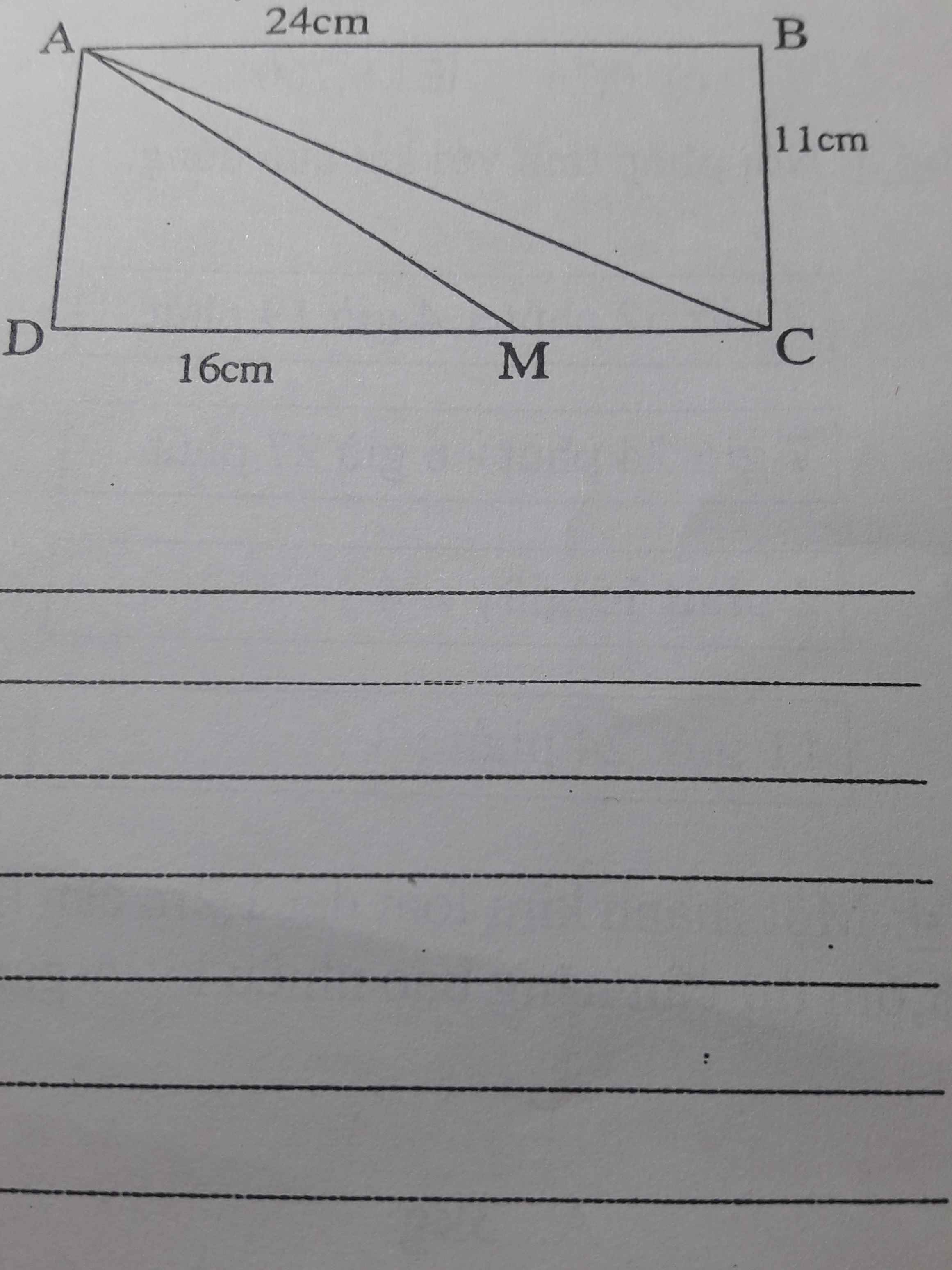
a) Diện tích hình chữ nhật \(ABCD\) là: \(24\times11=264\left(cm^2\right)\)
b) Diện tích hình tam giác \(ADM\) là: \(\dfrac{1}{2}\times11\times16=88\left(cm^2\right)\)
c) Diện tích hình tam giác \(ABC\) là: \(\dfrac{1}{2}\times24\times11=132\left(cm^2\right)\)
Diện tích hình tam giác \(AMC\) là: \(264-88-132=44\left(cm^2\right)\)