Cho tam giác ABC cân tại A, có \(\widehat{A}\) =120o , M là trung điểm của BC, qua C kẻ Cx song song với AM, Cx cắt BA tại E. AD là tia phân giác của góc AMC:
a) C/m: tam giác EAC đều
b) C/m: ED là trung trực của AC
c) C/m: DM<DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Bài này tôi search mạng chứ cs b lm đâu!!
1 tháng 4 2020
XÉT TAM GIÁC ABD VÀ TAM GIÁC AED
BA=EA ( GT)
\(\widehat{BAD}=\widehat{EAD}\)( GT)
AD-CẠNH CHUNG
=> TAM GIÁC ABD= TAM GIÁC AED ( C.G.C)
=>BD=BE ( 2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\widehat{ABD}=\widehat{AED}\)( 2 góc tương ứng )
b) ta có : \(\widehat{ABD}+\widehat{KBD}=180^o\left(kb\right)\)
cũng có ; \(\widehat{AED}+\widehat{CED}=180^o\left(kb\right)\)
mà \(\widehat{ABD}=\widehat{AED}\left(cmt\right)\)
=> \(\widehat{KBD}=\widehat{CED}\)
XÉT TAM GIÁC KBD VÀ TAM GIÁC CED :
\(\widehat{KBD}=\widehat{CED}\)(CMT)
BD=ED ( CMT)
\(\widehat{BDK}=\widehat{EDC}\)( ĐỐI ĐỈNH )
=> TAM GIÁC KBD = TAM GIÁC CED (G.C.G)
=>DK=DC ( 2 CẠNH TƯƠNG ỨNG)
c)
vì \(BC//KN\)(GT)
=>\(\widehat{CDN}=\widehat{DNK}\)(SO LE TRONG )
MÀ 2 GÓC NÀY LẠI Ở VỊ TRÍ SO LE TRONG CỦA KD VÀ NC
=> KD//NC
=> \(\widehat{KDN}=\widehat{CND}\)(SO LE TRONG)
XÉT TAM GIÁC KDN VÀ TAM GIÁC CND
\(\widehat{KDN}=\widehat{CND}\)( CMT)
DN-CẠNH CHUNG
\(\widehat{CDN}=\widehat{DNK}\)(CMT)
=> TAM GIÁC KDN = TAM GIÁC CND
=> KN = DC ( 2 CẠNH TƯƠNG ỨNG)
LẠI CÓ DC= DK ( CMT )
=> KN=DK
XÉT TAM GIÁC KDN:KN=DK
=> TAM GIÁC KDN CÂN TẠI K ( Đ/N)
1 tháng 4 2020
ặc olm có cái lỗi gì ý mình gửi bài mà nó mất tỏm đi mệt quá !!!!!!! mình chẳng muốn làm lại cả bài 2 và bài 3 một tí nào !!!!!!!!!!!!!!!!
KV
7 tháng 1
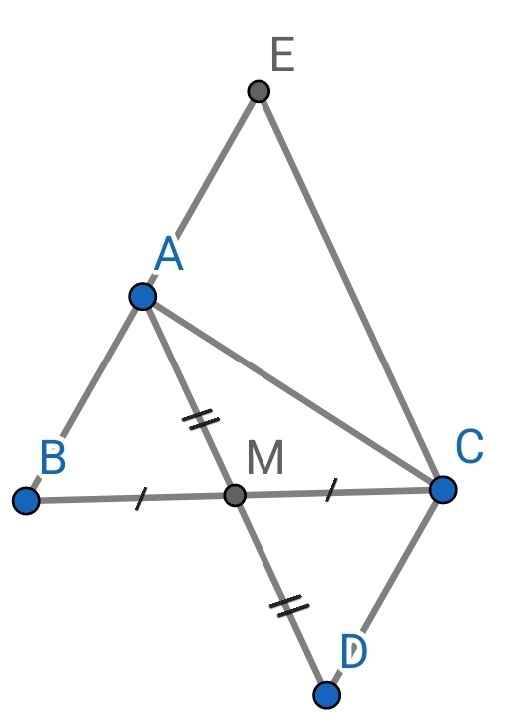a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE