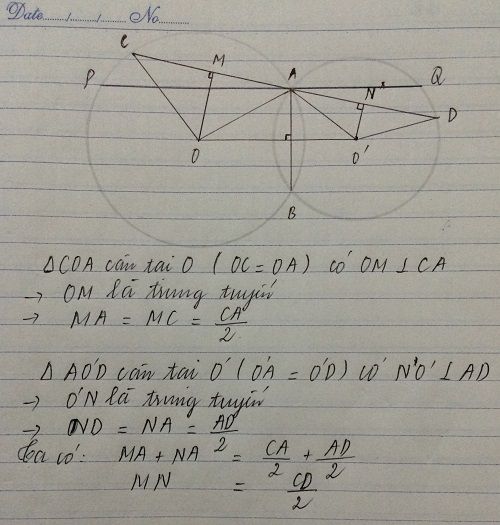Cho 2 đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến CAD và EAF với C và E thuộc đường tròn (O), D và F thuộc đường tròn (O') sao cho góc CAB=góc BAF. Chứng minh: CD = EF ...

TH

Thúy Hiền

31 tháng 3 2018 - olm

Cho 2 đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến CAD và EAF với C và E thuộc đường tròn (O), D và F thuộc đường tròn (O') sao cho góc CAB=góc BAF. Chứng minh: CD = EF Giúp e với ạ em cần...

Đọc tiếp

#Toán lớp 9

0

AL

An Lê

3 tháng 1

Cho 2 đường tròn (O) và (O') cắt nhau ở A và B (O và O' thuộc hai nửa mặt phẳng bờ AB).Qua A kẻ 2 cát tuyến CD và EF (C và E thuộc (O),D và F thuộc (O').Từ B kẻ BH vuông góc với CD,kẻ BK vuông góc với EF.Biết góc CAB bằng góc BAF. a.Chứng minh tam giác BHC bằng tam giác BKE b.So sánh CD và EF

#Toán lớp 9

0

HT

HUỲNH THỊ KIM HƯƠNG

7 tháng 12 2017 - olm

1. Cho hai đường tròn (O) và (O') cắt nhau tại A và B . Vẽ các cát tuyến chung CAD và EBF của hai đường tròn sao cho CD song song EF, C và E thuộc (O) , D và F thuộc (O') . Chứng minh CDFE là hình bình hành

#Toán lớp 9

0

BV

Bùi Việt Anh

23 tháng 11 2018 - olm

Cho 2 đường tròn (O) và (O') giao nhau ở A và B ( O và O' thuộc 2 nửa mặt phẳng bờ AB ). Một cát tuyển kẻ qua A cắt đường tròn (O) ở C, cắt đường tròn (O') ở D. Kẻ OM vuông góc CD và O'N vuông góc CD. a) CM MN=1/2 CDb) Gọi I là trung điểm của MN. CMR đường thẳng kẻ qua I vuông góc với CD luôn luôn đi qua một điểm cố định khi cát tuyến CAD thay đổic) Qua A kẻ cát tuyến // với đường nối tâm...

Đọc tiếp

#Toán lớp 9

4

NL

Nguyễn Linh Chi

23 tháng 11 2018

Chắc câu a và câu b dễ rồi

cô chỉ em làm câu c.

Gọi L là trung điểm AP K là trung điểm AQ

=> PQ=2LK=2OO'

Mà CD=2MN , MN<OO,

=> CD<OO'<PQ

Đúng(0)

BV

Bùi Việt Anh

24 tháng 11 2018

Tại sao MN lại bé hơn OO'

Đúng(0)

DQ

Dương Quỳnh Trang

9 tháng 1 2017 - olm

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A kẻ cát tuyến cắt đường tròn (O) tại C, cắt đường tròn (O') tại D sao cho CD vuông góc với AB, đường thẳng CB cắt đường tròn (O) tại M, đường thẳng DB cắt đường tròn (O') tại N. Chứng minh AB là tia phân giác của góc MAN

#Toán lớp 9

0

H

hellokittykute

28 tháng 5 2015 - olm

cho 2 đường tròn (O) và (O') cắt nhau tại A và B . trên nửa mặt phẳng bờ OO' chứa B,vẽ tiếp tuyến chung EF(E thuộc (O),F thuộc (O')).Một cát tuyến qua A và song song với EF cắt (O) tại C và cắt (O') tại D.Hai đường thẳng CE , DF cắt nhau tại I CMR : IA vuông góc với CD

#Toán lớp 8

0

PC

Pham Công Hạnh

6 tháng 2 2023

Cho đường tròn tâm O, cát tuyến (d) cắt đường tròn tại A và B, C thuộc (d) sao cho A nằm giữa C và B. từ C vẽ tiếp tuyến CN với đường tròn tại N (N thuộc cung lớn AB), CO cắt đường tròn tại E và F. Từ N hạn NI vuông góc với CO tại I. Chứng minh góc EIA = góc OAB

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

6 tháng 2 2023

Xét ΔCNO vuông tại N có NI là đường cao

nên CI*CO=CN^2

Xét ΔCNA và ΔCBN có

góc CNA=góc CBN

góc NCA chung

=>ΔCNA đồng dạng vơi ΔCBN

=>CN/CB=CA/CN

=>CN^2=CA*CB=CI*CO

=>CI/CB=CA/CO

=>ΔCIA đồng dạng với ΔCBO

=>góc CIA=góc CBO=góc OAB

Đúng(1)

HT

Huỳnh Trần Thảo Nguyên

13 tháng 7 2018 - olm

Cho đường tròn (O) và (O') cắt nhau tại A và B (O,O' thuộc 2 nửa mặt phẳng bờ AB), một cát tuyến kẻ qua A cắt (O) ở C, cắt (O') ở D. Kẻ OM vuông góc với CD, O'N vuông góc với CDa) Chứng minh: CD=2MNb) Gọi I là trung điểm của MN. Chứng minh: đường thẳng kẻ qua I vuông góc với BC đi qua 1 điểm cố định khi cát tuyến vẽ qua A thay đổic) Qua A kẻ cát tuyến // với đường nối tâm OO', cắt (O) tại P,...

Đọc tiếp

#Toán lớp 9

2

VD

Vũ Duy Hưng

13 tháng 7 2018

Cho (O) và (O') cắt nhau ở A và B,Một cát tuyến kẻ qua A cắt (O) ở C và cắt (O') ở D,Kẻ OM vuông góc với CD,O'N vuông góc CD,Chứng minh MN = 1/2CD,Gọi I là trung điểm của MN,đường thẳng kẻ qua I vuông góc với CD đi qua 1 điểm cố định,Toán học Lớp 9,bài tập Toán học Lớp 9,giải bài tập Toán học Lớp 9,Toán học,Lớp 9