x,y thỏa mãn 3x+2y=5. tìm giá trị lớn nhất E =xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 6 2019
Đáp án C.
Ta có
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ log 3 x + y - log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
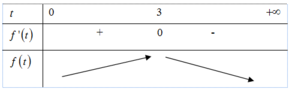
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ , có f ' t = 1 + 1 t ln 3 > 0 ; ∀ t > 0 .
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f[3(x + y)] = f(x2 + y2 + xy + 2)
CM
24 tháng 12 2018
Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.
CM
25 tháng 11 2019
Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
25 tháng 4 2018
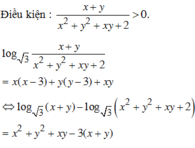
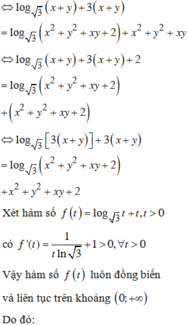
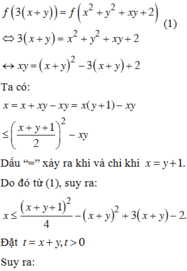
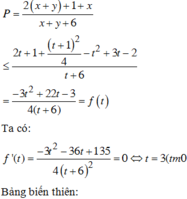
Câu hỏi của Phú Hồ Kim - Toán lớp 7 - Học toán với OnlineMath
tham khảo nhé
I
1 tháng 7 2020
Đặt \(a=3x^2+xy+2y^2=>0\le a\le2\)
xét 2 TH
+) Nếu a=0 thì x=y=0 nên P =0
+) nếu \(a\ne0\)thì x hoặc y phải khác 0
xét biểu thức
\(\frac{P}{a}=\frac{x^2+3xy-y^2}{3x^2+xy+2y^2}\)
nếu y=0 thì \(x\ne0=>\frac{P}{a}=\frac{1}{3}< P=\frac{a}{3}\le\frac{2}{3}\)
-xét TH y khác 0 , khi đó đặt \(t=\frac{x}{y}\), ta có
\(\frac{P}{a}=\frac{x^2+3xy-y^2}{3x^2+xy+2y^2}=\frac{t^2+3t-1}{3t^2+t+2}\)
gọi m là một giá trị \(\frac{P}{a}\), khi đó PT sau có nghiệm
\(m=\frac{t^2+3t-1}{3t^2+t+2}\)
\(=>\left(3m-1\right)t^2+\left(m-3\right)t+2m+1=0\left(1\right)\)
nếu \(m=\frac{1}{3}\left(thì\right)t=\frac{5}{8}.Nếu\left(m\ne\frac{1}{3}\right)thì\left(1\right)\)là PT bậc 2 có nghiệm khi zà chỉ khi
\(\left(m-3\right)^2-4\left(3m-1\right)\left(2m+1\right)\ge0\)
\(\Leftrightarrow23m^2+10m-13\le0\Leftrightarrow m\le\frac{13}{23}=>-1\le\frac{P}{a}\le\frac{26}{23}\)
mà a>0 nên \(-2\le-a\le P\le\frac{13}{23}a\le\frac{26}{23}\)
kết hợp những TH zừa xét lại ta có
\(-2\le P\le\frac{26}{23}\)
I
1 tháng 7 2020
làm tiếp nè , mình phải làm tách ra không sợ nó lag
\(P=-2\)khi zà chỉ khi
\(\hept{\begin{cases}\frac{x}{y}=\frac{3-m}{2\left(3m-1\right)}=-\frac{1}{2}\\3x^2+xy+2y^2=2\end{cases}\Leftrightarrow\hept{\begin{cases}y=-2x\\3x^2-2x^2+8x^2=2\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}y=-2x\\x=\pm\frac{\sqrt{2}}{3}\end{cases}\Leftrightarrow\hept{\begin{cases}x=\pm\frac{\sqrt{2}}{3}\\y=\mp\frac{2\sqrt{2}}{3}\end{cases}}}\)
zậy MinP=-2 khi ....
+) MaxP nhé
\(P=\frac{26}{13}\)khi
\(\hept{\begin{cases}\frac{x}{y}=\frac{3-m}{2\left(3m-1\right)}=\frac{7}{4}\\3x^2+xy+2y^2=2\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{7}{4}y\\3\left(\frac{7}{4}y\right)+\frac{7}{4}y^2+2y^2=2\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{7}{4}y\\y=\pm\frac{4}{3}\sqrt{\frac{2}{23}}\end{cases}\Leftrightarrow\hept{\begin{cases}x=\pm\frac{7}{3}\sqrt{\frac{2}{23}}\\y=\pm\frac{4}{3}\sqrt{\frac{2}{23}}\end{cases}}}\)
zậy ....
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
\(x\ge xy+1\Rightarrow1\ge y+\dfrac{1}{x}\ge2\sqrt{\dfrac{y}{x}}\Rightarrow\dfrac{y}{x}\le\dfrac{1}{4}\)
\(Q^2=\dfrac{x^2+2xy+y^2}{3x^2-xy+y^2}=\dfrac{\left(\dfrac{y}{x}\right)^2+2\left(\dfrac{y}{x}\right)+1}{\left(\dfrac{y}{x}\right)^2-\dfrac{y}{x}+3}\)
Đặt \(\dfrac{y}{x}=t\le\dfrac{1}{4}\)
\(Q^2=\dfrac{t^2+2t+1}{t^2-t+3}=\dfrac{t^2+2t+1}{t^2-t+3}-\dfrac{5}{9}+\dfrac{5}{9}\)
\(Q^2=\dfrac{\left(4t-1\right)\left(t+6\right)}{9\left(t^2-t+3\right)}+\dfrac{5}{9}\le\dfrac{5}{9}\)
\(\Rightarrow Q_{max}=\dfrac{\sqrt{5}}{3}\) khi \(t=\dfrac{1}{4}\) hay \(\left(x;y\right)=\left(2;\dfrac{1}{2}\right)\)
CM
28 tháng 10 2019
Đáp án C
Ta có: 9 x 2 − 4 y 2 = 5 ⇔ 3 x + 2 y 3 x − 2 y = 5 ⇔ 3 x − 2 y = 5 3 x + 2 y
Khi đó: log m 3 x + 2 y = log 3 3 x − 2 y = 1
⇔ log m 3 x + 2 y − log 3 5 3 x + 2 y = 1
⇔ log m 3 x + 2 y + log 3 3 x + 2 y − log 3 5 = 1 ⇔ log m 3. log 3 3 x + 2 y + log 3 3 x + 2 y = log 3 15 ⇔ log 3 3 x + 2 y 1 + log m 3 = log 3 15
Vì 3 x + 2 y ≤ 5
nên log 3 3 x + 2 y ≤ log 3 5 ⇒ log 3 15 1 + log m 3 ≤ log 3 5
⇔ log 3 15 log 3 5 ≤ 1 + log m 3
⇔ log m 3 ≥ log 5 15 − 1 = log 5 3 ⇔ m ≤ 5.
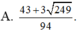
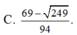
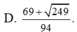
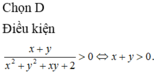
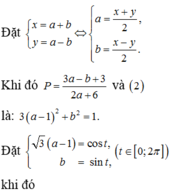
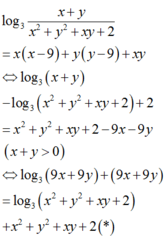
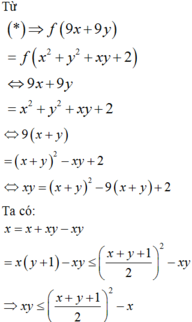
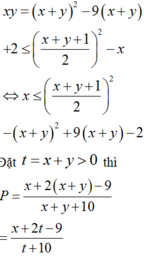
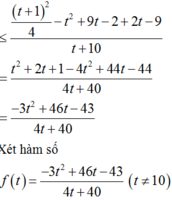
3x+2y=5 => y = (5-3x)/2
E=xy = x(5-3x)/2
=> 2E=5x-3x2 = -3(x2-5x/3)
=> \(2E=-3\left(x^2-2.\frac{5}{6}x+\frac{25}{36}-\frac{25}{36}\right)\)
=> \(2E=\frac{25}{12}-3\left(x-\frac{5}{6}\right)^2\)
Nhận thấy: \(\left(x-\frac{5}{6}\right)^2\ge0\) Với mọi x
=> Giá trị lớn nhất của 2E là 25/12, đạt được khi x=5/6
=> \(E_{min}=\frac{25}{24}\) đạt được khi x=5/6