Tìm nghiệm của các đa thứ sau:
a) 4x2 - 18xx
b) x2 - 112x
c) 2/5x2 - 5/2
d) 2x(x - 1/2) - x(2x + 5)
e) 7/3x(9 - x) - 12x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2020
Bài 1:
a) (3x - 2)(4x + 5) = 0
<=> 3x - 2 = 0 hoặc 4x + 5 = 0
<=> 3x = 2 hoặc 4x = -5
<=> x = 2/3 hoặc x = -5/4
b) (2,3x - 6,9)(0,1x + 2) = 0
<=> 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
<=> 2,3x = 6,9 hoặc 0,1x = -2
<=> x = 3 hoặc x = -20
c) (4x + 2)(x^2 + 1) = 0
<=> 4x + 2 = 0 hoặc x^2 + 1 # 0
<=> 4x = -2
<=> x = -2/4 = -1/2
d) (2x + 7)(x - 5)(5x + 1) = 0
<=> 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
<=> 2x = -7 hoặc x = 5 hoặc 5x = -1
<=> x = -7/2 hoặc x = 5 hoặc x = -1/5
CM
8 tháng 9 2018
a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: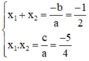 
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: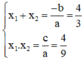 
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: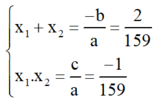 
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Bạn cần viết đề bằng công thức toán để được hỗ trợ tốt hơn.
12 tháng 10 2023
a: \(x^2+4x+4=x^2+2\cdot x\cdot2+2^2=\left(x+2\right)^2\)
b: \(4x^2-4x+1=\left(2x\right)^2-2\cdot2x\cdot1+1^2=\left(2x-1\right)^2\)
c: \(2x-1-x^2\)
\(=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
d: \(x^2+x+\dfrac{1}{4}=x^2+2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2\)
e: \(9-x^2=3^2-x^2=\left(3-x\right)\left(3+x\right)\)
g: \(\left(x+5\right)^2-4x^2=\left(x+5+2x\right)\left(x+5-2x\right)\)
\(=\left(5-x\right)\left(5+3x\right)\)
h: \(\left(x+1\right)^2-\left(2x-1\right)^2\)
\(=\left(x+1+2x-1\right)\left(x+1-2x+1\right)\)
\(=3x\left(-x+2\right)\)
i: \(=x^2y^2-4xy+4-3\)
\(=\left(xy-2\right)^2-3=\left(xy-2-\sqrt{3}\right)\left(xy-2+\sqrt{3}\right)\)
k: \(=y^2-\left(x-1\right)^2\)
\(=\left(y-x+1\right)\left(y+x-1\right)\)
l: \(=x^3+3\cdot x^2\cdot2+3\cdot x\cdot2^2+2^3=\left(x+2\right)^3\)
m: \(=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot y+3\cdot2x\cdot y^2-y^3=\left(2x-y\right)^3\)
CW
25 tháng 1 2017
a) \(4x^2-7x+5=\left(x+2\right)\left(2x-9\right)\)
\(\Leftrightarrow4x^2-7x+5=2x^2-5x-18\)
\(\Leftrightarrow2x^2-2x+23=0\)
\(\Rightarrow\Delta=b^2-4ac=\left(-2\right)^2-4\cdot1\cdot23=-732< 0\)
Vậy pt vô nghiệm
b) \(-x^2-12x+21=\left(3-x\right)\left(x+11\right)\)
\(\Leftrightarrow-x^2-12x+21=-x^2-8x+33\)
\(\Leftrightarrow4x+12=0\Leftrightarrow x=-3\)
c) \(9x+5x^2+1=5x^2-22+13x\)
\(\Leftrightarrow4x-23=0\Leftrightarrow x=\frac{23}{4}\)
2 tháng 7 2023
4:
a: f(x)=0
=>-x-4=0
=>x=-4
b: g(x)=0
=>x^2+x+4=0
Δ=1^2-4*1*4=1-16=-15<0
=>g(x) ko có nghiệm
c: m(x)=0
=>2x-2=0
=>x=1
d: n(x)=0
=>7x+2=0
=>x=-2/7
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
a.
\(1-4x^2=\left(1-2x\right)\left(1+2x\right)\)
b.
\(8-27x^3=\left(2\right)^3-\left(3x\right)^3=\left(2-3x\right)\left(4+6x+9x^2\right)\)
c.
\(27+27x+9x^2+x^3=x^3+3.x^2.3+3.3^2.x+3^3\)
\(=\left(x+3\right)^3\)
d.
\(2x^3+4x^2+2x=2x\left(x^2+2x+1\right)=2x\left(x+1\right)^2\)
e.
\(x^2-y^2-5x+5y=\left(x-y\right)\left(x+y\right)-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-5\right)\)
f.
\(x^2-6x+9-y^2=\left(x-3\right)^2-y^2=\left(x-3-y\right)\left(x-3+y\right)\)
a) Cho 4x^2-18x=0
=> x(4x-18)=0
=> x=0 hoặc 4x-18=0
=> x=0 hoặc x=18/4
Vậy x=0 và x=18/4 là nghiệm của đa thức trên.
b) Cho: x^2-112x=0
=> x(x-112)=0
=> x=0 hoặc x-112=0
=> x=0 hoặc x=112
Vậy x=0 và x=112 là nghiệm của đa thức trên.
c) Cho: 2/5x^2-5/2=0
=> 2/5x^2=5/2
=> x^2=25/4
<=> x=5/2 và -5/2
Vậy x=5/2 và x=-5/2 là nghiệm của đa thức trên.
Tương tự câu d và e bạn cũng cho đa thức đó = 0 là sẽ tìm ra giá trị của x.
Tính giá trị các đa thức sau tại x=-1x=−1?
a) P(x)=x^2 + x^4 + x^6 + x^8 + ... + x^{112}P(x)=x2+x4+x6+x8+...+x112.
P(-1)=P(−1)=.
b) Q(x)=x + x^3 + x^5 + x^7 + ... + x^{113}Q(x)=x+x3+x5+x7+...+x113.
Q(-1)=Q(−1)=.