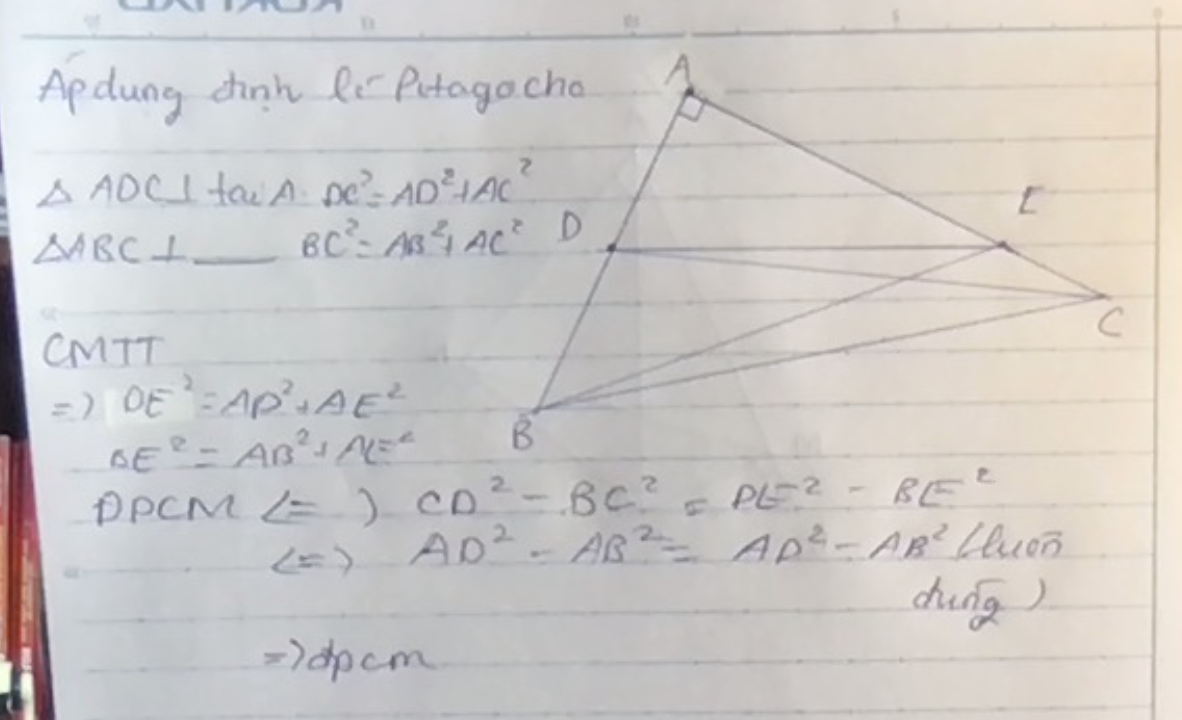
cho tam giác ABC vuông ở A .mooth dường thẳng cắt hai cạnh AB,AC lần lượt tại D,E .c/m rằng CD2-CB2=DE2-EB2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 11 2023
1: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>AH=DE
2: \(\widehat{EDM}=90^0\)
=>\(\widehat{EDH}+\widehat{MDH}=90^0\)
=>\(\widehat{EAH}+\widehat{MDH}=90^0\)
=>\(\widehat{MDH}+\widehat{HAC}=90^0\)
=>\(\widehat{MDH}+\widehat{ABC}=90^0\)
mà \(\widehat{MHD}+\widehat{MBD}=90^0\)
nên \(\widehat{MDH}=\widehat{MHD}\)
=>MD=MH
\(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)
\(\widehat{MHD}+\widehat{MBD}=90^0\)(ΔHDB vuông tại D)
mà \(\widehat{MDH}=\widehat{MHD}\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
=>MB=MH
=>M là trung điểm của BH
\(\widehat{NED}=90^0\)
=>\(\widehat{NEH}+\widehat{DEH}=90^0\)
=>\(\widehat{NEH}+\widehat{DAH}=90^0\)
mà \(\widehat{DAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{NEH}+\widehat{C}=90^0\)
mà \(\widehat{NHE}+\widehat{C}=90^0\)(ΔHEC vuông tại E)
nên \(\widehat{NEH}=\widehat{NHE}\)
=>NE=NH
\(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)
\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)
mà \(\widehat{NHE}=\widehat{NEH}\)
nên \(\widehat{NEC}=\widehat{NCE}\)
=>NE=NC
mà NH=NE
nên NC=NH
=>N là trung điểm của HC
3 tháng 12 2021
a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2022
Áp dụng định lý Pitago cho tam giác vuông ACD:
\(CD^2=AD^2+AC^2\)
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(CB^2=AB^2+AC^2\)
\(\Rightarrow CD^2-CB^2=AD^2+AC^2-AB^2-AC^2=AD^2-AB^2\) (1)
Áp dụng định lý Pitago cho tam giác vuông ADE:
\(ED^2=AD^2+AE^2\)
Áp dụng định lý Pitago cho tam giác vuông ABE:
\(EB^2=AB^2+AE^2\)
\(\Rightarrow ED^2-EB^2=AD^2+AE^2-AB^2-AE^2=AD^2-AB^2\) (2)
(1);(2) \(\Rightarrow CD^2-CB^2=ED^2-EB^2\)
15 tháng 2 2022
Ta cần CM: \(CD^2-CB^2=ED^2-EB^2\Leftrightarrow CD^2-AB^2-AC^2=ED^2-EB^2\Leftrightarrow EB^2-AB^2=ED^2-\left(CD^2-AC^2\right)\Leftrightarrow AE^2=ED^2-AD^2\left(luônđúng\right)\) (vì các tam giác ACD, ABE,ADE đều vuông tại A) \(\Rightarrowđpcm\)
5 tháng 3 2022
a: Xét ΔBEC và ΔCDB có
BE=CD
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔBEC=ΔCDB
Suy ra: CE=DB
b: Xét ΔGBC có \(\widehat{GCB}=\widehat{GBC}\)
nên ΔGBC cân tại G
=>GB=GC
Ta có: GB+GD=BD
GE+GC=CE
mà BD=CE
và GB=GC
nên GD=GE
hay ΔGDE cân tại G
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: GB=GC
nên G nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,G,M thẳng hàng