Cho tam giác ABC có góc A= 120 độ. Vẽ các đường phân giác AD, BE. Tính góc BED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TN
1

21 tháng 7 2016
Lời giải. Kẻ tia Ax là tia ối của tia AB, ta có dBAD= dCAD=
A
B D C
E
1 2 1 2
x
60 nên dCAx = 60.
Xét tam giác ABD có AE là phân giác ngoài tại ỉnh A,BD
là phân giác trong tại ỉnh B. Do ó DE là phân giác ngoài
tại ỉnh D. Do ó
[BED = cD1−cB1 =
dADC−dABC
2
=
dBAD
2
=
60
2
= 30.
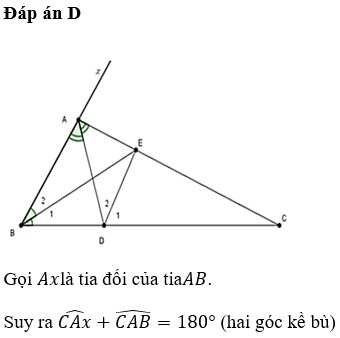



kẻ̉̉̉ tia Ax là tia đố́́́́́i củ̉̉̉a tia AC góc CAB=120 độ̣ =2góc CAD=2DAB => góc xAC =60 độ =>AC là pg củ̉̉a xAD; BE là pg cua gócABC mà BE cắt AC tạ̣i E =>DElà pg cua góc ADC =>góc DEB =góc EDC - EDB = ADC/2 - ABD/2 =120 - ADC/2 -60 - ACD/2 =120 /2 -60/2=30độ̣
kẻ̉̉̉ tia Ax là tia đố́́́́́i củ̉̉̉a tia AC \(\widehat{CAB}=120^o\)\(=2\widehat{CAD}=2\widehat{DAB}\) \(\Rightarrow\widehat{XAC}=60^o\) =>AC là phân giác củ̉̉a \(\widehat{XAD}\); BE là phân giác của \(\widehat{ABC}\) mà BE cắt AC tạ̣i E =>DE là phân giác cua \(\widehat{ADC}\) \(\Rightarrow\widehat{DEB}=\widehat{EDC}-\widehat{EDB}\) = \(\widehat{\frac{ADC}{2}}-\widehat{\frac{ABD}{2}}\) \(=120^o-\widehat{\frac{ADC}{2}}-60^o-\frac{\widehat{ACD}}{2}\) \(=\frac{120^o}{2}-\frac{60^o}{2}=30^o\)