Cho điểm O nằm trên đường thẳng AB. Trện nửa mặt phẳng bờ AB ta vẽ góc xOA, trên nửa mặt phẳng đối ta vẽ góc yOB.
a)Tìm điều kiện để tia đối của tia phân giác góc xOA là tia phân giác của goc YOB.
b)Với điều kiện đã tìm được ở phần a chứng minh rằng hai tia phân giác của góc xOB và yOB vuông góc với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 11 2019
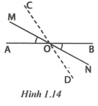
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác
30 tháng 4 2015
câu d mik từng giải 1 lần nhưng ko biết đúng/ sai, ai biết thì giả thử xem
10 tháng 6 2016
a) (Sửa lại là xOy và x'Oy' đối đỉnh nha, k có t trog đề bài 
)
Ta có : \(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-45^o=135^o\)
Oy là tia phân giác của góc x'Oy' nên \(\widehat{x'Oy'}=\frac{1}{2}\widehat{x'Oz}=\frac{1}{2}.90^o=45^o\)
Do đó \(\widehat{x'Oy}+\widehat{x'Oy'}=135^o+45^o=180^o\) => Oy, Oy' là 2 tia đối nhau (1)
; đã có điểm O trên đg thẳng xx' nên Ox, Ox' đối nhau (2)
Từ (1) và (2) => góc xOy và x'Oy' đối đỉnh
b) Ta có : \(\widehat{xOy}+\widehat{yOt}+\widehat{x'Ot}=180^o\) (kề bù)
=> \(\widehat{x'Ot}=180^o-45^o-90^o=45^o\)