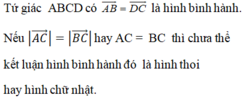cho tứ giác abcd(ab//dc,ab<dc) cm: ad=be,ab=de;dc-ab=ec;ad+bc>dc-ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
31 tháng 5 2018
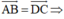tứ giác ABCD là hình bình hành
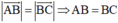
⇒ tứ giác ABCD là hình thoi.
(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)
BT
0
PC
2
NM
21 tháng 6 2016
AB+BD\(\le\)AC+DC
=> AC - AB\(\ge\) BD-DC ma BD>CD ( Tu giac loi co duong cheo > canh)
=> AC-AB> hay AC> AB
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
VH
0