tìm các chữ số a;b;c;d biết ab x cd = ddd
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b) để a4b ⋮ 2 và 5
thì b=0
để a40 ⋮ 3 và 9 thì tổng các chữ số phải ⋮ 9
⇒ \(\left(a+4\right)\text{⋮}9\)
⇒ \(a=5\)
Vậy a=5, b=0
c) để 2a5b ⋮5 thì b=0 hoặc 5
Nếu b=0 thì a=2
Nếu b=5 thì a=7
Vậy (a,b)=\(\left\{\left(2;0\right);\left(7;5\right)\right\}\)

Bài 7:
a: \(24=2^3\cdot3\)
b: \(75=5^2\cdot3\)
c: \(300=2^2\cdot3\cdot5^2\)
d: \(520=2^3\cdot5\cdot13\)
Bài 6:
a:
Sửa đề: 56ab
Đặt \(X=\overline{56ab}\)
X chia hết cho 2 và 5 nên X chia hết cho 10
=>X có tận cùng là 0
=>b=0
=>\(X=\overline{56a0}\)
X chia hết cho 3 và 9 nên X chia hết cho 9
=>5+6+a+0 chia hết cho 9
=>a+11 chia hết cho 9
=>a=7
=>X=5670
b: Đặt \(X=\overline{3ab}\)
X chia hết cho 2 và 5 nên X chia hết cho 10
=>b=0
=>\(X=\overline{3a0}\)
X chia hết cho 3 và 9 nên X chia hết cho 9
=>3+a+0 chia hết cho 9
=>a=6
=>X=360
c: Đặt \(X=\overline{1a2b}\)
X chia hết cho 5 nên b=0 hoặc b=5
TH1: b=0
=>\(X=\overline{1a20}\)
X chia hết cho 9
=>1+a+2+0 chia hết cho 9
=>a+3 chia hết cho 9
=>a=6
=>X=1620
TH2: b=5
=>\(X=\overline{1a25}\)
X chia hết cho 9
=>1+a+2+5 chia hết cho 9
=>a+8 chia hết cho 9
=>a=1
=>X=1125

a: 0,1246
b:
Sửa đề: Có tích các chữ số bằng 48
Số cần tìm là 8,321

a tích các chữ số có 1 chữsố bằng 120 là
120 = 3x5x8
vậy số tự nhiên bé nhất có tích là 120 là 385
nhớ kic cho mik nhé
nhưng bài này sai thôi tớ ko biết đâu

- ta có 10a + b +10b +a =176
<=> 10(a+b) +a +b =176
<=> 11(a+b) =176
<=> a + b =16
=> a=7 và b=9 hoặc a=9 và b=7 (vì a khác b)
- Theo đề ta có : c+b=c =>b=0
Vì ac và cb là số có hai chữ số => a=1
=> 10 +c +10c = 100 + c
=> 10c = 90
=>c=9
Vậy số cần tìm là 109
Bài 1:
Giải:
Ta có:
\(\overline{ab}+\overline{bc}=176\)
\(\Rightarrow10a+b+10b+a=176\)
\(\Rightarrow11a+11b=176\)
\(\Rightarrow11\left(a+b\right)=176\)
\(\Rightarrow a+b=16\)
Vì a, b là chữ số nên ta có bảng sau:
| a | 7 | 9 | 8 |
| b | 9 | 7 | 8 |
Vậy các cặp số \(\left(a;b\right)\) là: \(\left(7;9\right);\left(9;7\right);\left(8;8\right)\)

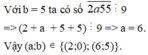
ab x cb = ddd
b x b = d nên d chỉ có thể là 4; 6 hoặc 9, khi đó b sẽ là 2; 4; 3 hoặc 7
Vì hai thừa số là số có hai chữ số và tích có ba chữ số bằng nhau, nên chữ số hàng chục sẽ bé hơn hàng đơn vị.
Vì vậy ta chọn b = 7
Nếu b = 7 và d = 9 ta có: a7 x c7 = 999
( Ta thấy 7 x 7 = 49, viết 9 nhớ 4. Vậy chọn a là số mà khi nhân 7, cộng thêm 4 rồi cộng thêm ở c x 7 để có kết quả là 9 )
Thế vào phép tính suy ra ta có:
a = 2 và c = 3
27 x 37 = 999
Vậy abcd = 2739
ab x cd = ddd = d x 111 = d x 3 x 37, mà 37 là số nguyên tố
=> ab = 37 hoặc cd = 37
TH1: nếu cd = 37 thì:
ab x 37 = 777
=> ab = 21
TL: 21.37 = 777 (thỏa mãn)
TH2: nếu ab = 37 thì:
37 x cd = d x 3 x 37
=> cd = d x 3
Ta thấy : cd <= 27 (vì d <= 9 => cd <= 27)
mà c > 0 nên c = 1 hoặc c = 2
+) Nếu c = 1 => 10 + d = 3d
=> 10 = 2d
=> d = 5
TL: 37.15 = 555 (thỏa mãn)
+) Nếu c = 2 => 20 + d = 3d
=> 20 = 2d
=> d = 10 (loại vì d là chữ số)
ĐS: (a; b; c; d) ∈ {(3;7;1;5);(2;1;3;7)}