tìm a,b.c không âm biết c + 3a=2016;c+2b=2018 và tổng a+b+c có giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2020
câu 1
xét tích 3 số
=(3a^2.b.c^3).(-2a^3b^5c).(-3a^5.b^2.c^2)
=[3.(-2).(-3)].(a^2.a^3.a^5).(b.b^5.b^2).(c.c^3.c^2)
=18.a^10.b^8.c^5 bé hơn hoặc bằng 0
=>tích 3 số đó không thể cùng âm=>3 số đó ko cùng âm dc
bây giờ mk đi học rùi tí về mk làm típ nhá
J
1
5 tháng 12 2019
3a+4b-3c=4. Tìm GTNN của biểu thức : A = 2a+3b-4c? ... Cho a;b;c là các số không âm thỏa mãn:2a+b=6-3c;3a+4b=3c+4.Tìm min ... T = a −2 b 2 a − b +2 a −3 b 2 a + b. Đọc tiếp. ..... cho a và b là hai số thực thỏa mãn 4a + b = 5ab và 2a>b>0.
DN
3
H
11 tháng 7 2021
Điều phải chứng minh tương đương với
\(2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\\ \Leftrightarrow\left(a+b-2\sqrt{ab}\right)+\left(b+c-2\sqrt{bc}\right)+\left(c+a-2\sqrt{ca}\right)\ge0\\ \Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)
(luôn đúng với mọi a,b,c không âm)
Dấu = xảy ra khi a=b=c >=0
PQ
1
21 tháng 1 2019
làm lại cho dễ hiểu.
Ta có:\(\hept{\begin{cases}a+3c=2016\left(1\right)\\a+2b=2017\left(2\right)\end{cases}}\)
Từ (1) \(\Rightarrow a=2016-3c\)
Lấy (2)-(1),ta được:
\(2b-3c=1\)
\(\Rightarrow b=\frac{1+3c}{2}\)
Khi đó:\(P=a+b+c\)
\(=\left(2016-3c\right)+\frac{1+3c}{2}+c\)
\(=\left(2016+\frac{1}{2}\right)+\frac{-6c+3c+2c}{2}\)
\(=2016\frac{1}{2}-\frac{c}{2}\)
Vì a,b,c không âm nên:
\(P=2016\frac{1}{2}-\frac{c}{2}\)
\(\le2016\frac{1}{2}\)
\(\Rightarrow P_{MAX}=2016\frac{1}{2}\)tại \(c=0\)
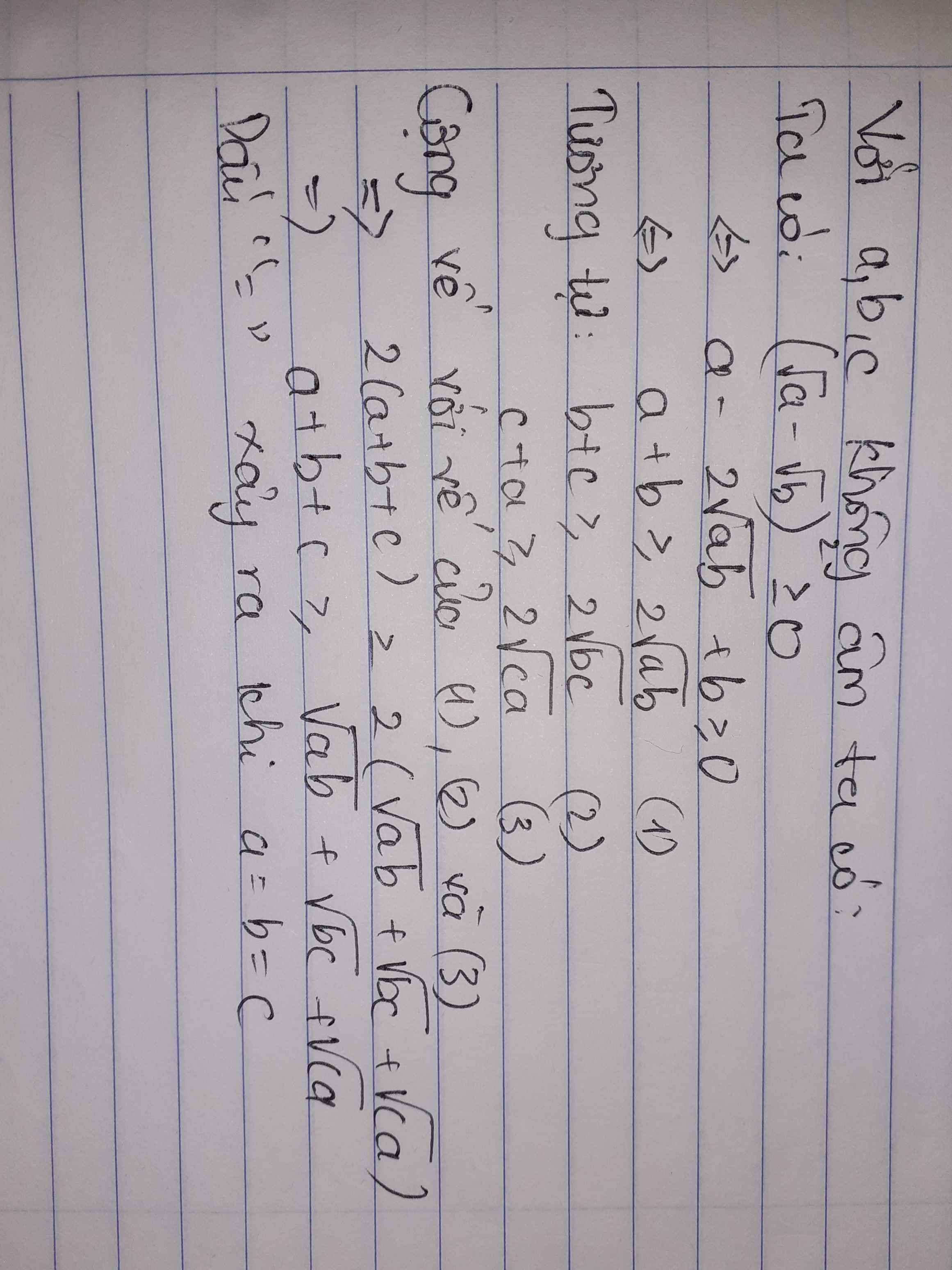
\(c+3a=2016\Leftrightarrow a=\frac{2016-c}{3}\ge0\Leftrightarrow c\le2016\)
\(c+2b=2018\Leftrightarrow b=\frac{2018-c}{2}\Leftrightarrow c\le2018\)
\(a+b+c=\frac{2016-c}{3}+\frac{2018-c}{2}+c\)
\(=\frac{2016}{3}+\frac{2018}{2}+\frac{c}{6}\le\frac{2016}{3}+1009+\frac{2016}{6}=2017\)
Dấu \(=\)khi \(c=2016\Rightarrow a=0,b=1\).