Tìm giá trị của biến để các biểu thức sau có nghĩa; căn bậc 2 của x^2 +3 Tìm x: căn bậc 2 của x-3 phần x+1 và căn bậc 2 của 4x^2-4x+1 cộng cho căn bậc 2 của 2x-1=0 Rút gọn: C=căn bậc 2 của x-1-2* căn bậc 2 của x-2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
14 tháng 5 2021
ĐK để căn có nghĩa:
`-4x^2+4x-2>=0`
`<=>2x^2-2x+1<=0`(vô lý)
Vì `2x^2-2x+1=2(x-1/2)^2+1/2>0`
`=>` không có gtrij của x thỏa đề bài.
D
6
GH
28 tháng 6 2023
c
Để biểu thức C có nghĩa thì
\(\sqrt{x\sqrt{2x-1}}>0\)
<=> \(\left\{{}\begin{matrix}x>0\\2x-1>0\Leftrightarrow x>\dfrac{1}{2}\end{matrix}\right.\Rightarrow x>\dfrac{1}{2}\)
Vậy để biểu thức C có nghĩa thì \(x>\dfrac{1}{2}\)
Giải câu e:
Điều kiện để biểu thức E có nghĩa:
\(\left\{{}\begin{matrix}x+\dfrac{2}{x}\ge0\\-2x\ge0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}\dfrac{x^2+2}{x}\ge0\\x\le0\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x>0\\x\le0\end{matrix}\right.\)
Vậy không tồn tại x để biểu thức E có nghĩa.
TN
19 tháng 5 2021
a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
TN
19 tháng 5 2021
Mình làm sai câu a...
Ta có: \(M=\dfrac{8x+1}{4x-1}=\dfrac{8x-2+3}{4x-1}=\dfrac{2\left(4x-1\right)+3}{4x-1}=2+\dfrac{3}{4x-1}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{3}{4x-1}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{3}{4x-1}\) nhận giá trị nguyên
Vì \(4x-1\in Z\) nên \(4x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow x\in\left\{\pm0,5;0;1\right\}\)
Vậy \(x\in\left\{0;1\right\}\) thỏa mãn \(x\in Z\).
H
1
23 tháng 3 2022
a.\(16-x^2=0\)
\(\Leftrightarrow x^2=16\)
\(\Leftrightarrow x^2=4^2\)
\(\Leftrightarrow x=\pm4\)
b.\(\left(x+1\right)^2+\left(2y-3\right)^{10}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\\left(2y-3\right)^{10}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2y-3=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{2}\end{matrix}\right.\)
CM
28 tháng 6 2019
xác định khi:
(x + y)(6x – 6y)
≠
0 ⇒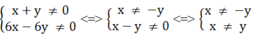 
Điều kiện x ≠ ± y
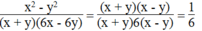
Vậy biểu thức không phụ thuộc vào x, y.
CM
21 tháng 1 2017
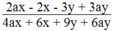xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
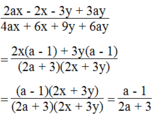
Vậy biểu thức không phụ thuộc vào x, y.
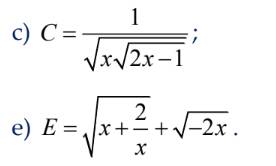
Bạn cần viết lại đề bằng công thức toán (gõ công thức trong hộp có biểu tượng $\sum$) để được hỗ trợ tốt hơn. Nhìn đề thế này rối mắt quá.