cho hình tam giác abc có ae=ec;bd=1/3bc;diện tích hình tam giác dec là 6cm2 . tính diện tích hình tam giác abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PL
8 tháng 6 2018
Nối C với D.Ta thấy CBD hay CDA =1/2 ABC=ABC:2=90:2=45(cm vuông)
Ta thấy AKD,KED,ECD có chung đường cao và đều có đáy =1/3 đáy AC. Vậy suy ra các hình AKD,KED,ECD=1/3CDA=45:3=15(cm vuông)
AED=2/3 CDA=45x2/3=30 (cm vuông) hoặc AED=ADK+EKD=15+15=30(cm vuông)
Đ/S:30 cm vuông
5 tháng 3 2017
Kết quả bài này là 90 cm2
Giải bài này dài lắm nên mk ko giải ra đc đâu
3 tháng 6 2016
Nối C với D. Ta thấy CBD hay CDA = 1/2 ABC = ABC : 2 = 90 : 2 = 45 ( cm2 )
Ta thấy AKD, KED, ECD có chung đường cao và đều có đáy = 1/3 đáy AC. Vậy suy ra các hình AKD, KED, ECD = 1/3 CDA = 45 : 3
= 15 ( cm2 )
AED = 2/3 CDA = 45 x 2/3 = 30 ( cm2 ) hoặc AED = ADK + EKD = 15 + 15 = 30 ( cm2 )
Đáp số : 30 cm2
KV
7 tháng 12 2023
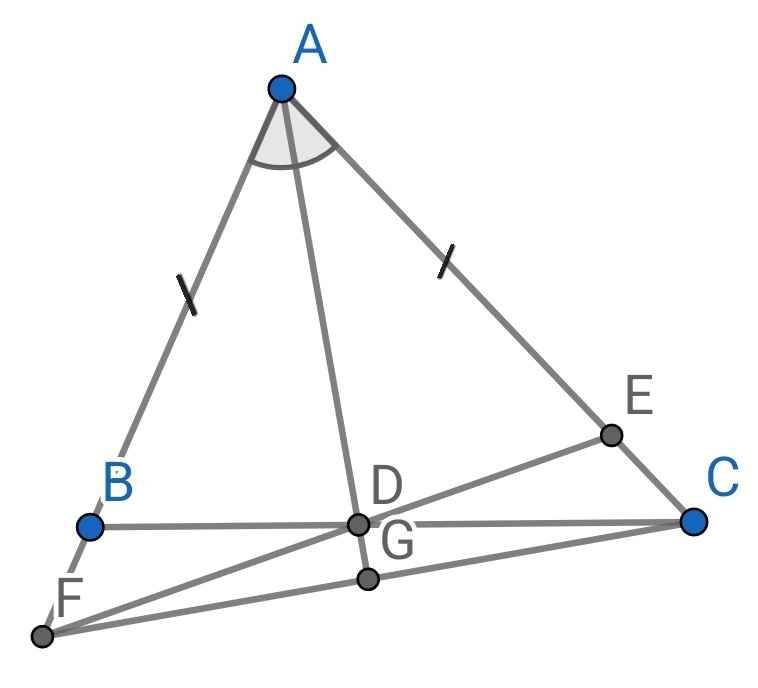a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ BD = ED (hai cạnh tương ứng)
Do ∆ABD = ∆AED (cmt)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
Ta có:
∠ABD + ∠FBD = 180⁰ (kề bù)
∠AED + ∠CED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Xét ∆BDF và ∆EDC có:
BD = ED (cmt)
∠FBD = ∠CED (cmt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (g-c-g)
b) Do ∆BDF = ∆EDC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
c) Gọi G là giao điểm của AD và CF
AG là tia phân giác của ∠FAC
⇒ ∠FAG = ∠CAG
Xét ∆AFG và ∆ACG có:
AF = AC (gt)
∠FAG = ∠CAG (cmt)
AG là cạnh chung
⇒ ∆AFG = ∆ACG (c-c-c)
⇒ ∠AGF = ∠AGC (hai góc tương ứng)
Mà ∠AGF + ∠AGC = 180⁰ (kề bù)
⇒ ∠AGF = ∠AGC = 180⁰ : 2 = 90⁰
⇒ AG FC
Hay AD ⊥ FC