cho a.c=b^2;b.d=c^2 và a,b,c,d khác 0. Chừng minh rằng: a^3.d+b^3.d+c^3.d=a.b^3+c^3.a+a.d^3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
0
TT
0
AH
30 tháng 10 2016
\(\frac{a+b}{a-b}=\frac{a+c}{c-a}\)
=> ( a + b ) ( c -a ) = ( a + c ) ( a - b )
=> a ( c - a ) + b ( c - a ) = a ( a - b ) + c ( a - b )
=> ac - aa + bc - ba = aa - ab + ca - bc
=> - aa - aa = - bc - bc
=> - 2 a 2 = - 2 bc
=> a 2 = bc
Vậy \(\frac{a+b}{a-b}=\frac{a+c}{c-a}\)thì a 2 = bc
18 tháng 10 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\\ \dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\\ \Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{ac}{bd}\)
26 tháng 8 2021
Đề sai rồi bạn. Phải thay "^2" bằng "^3" mới đúng.
HD
1
VM
8 tháng 11 2019
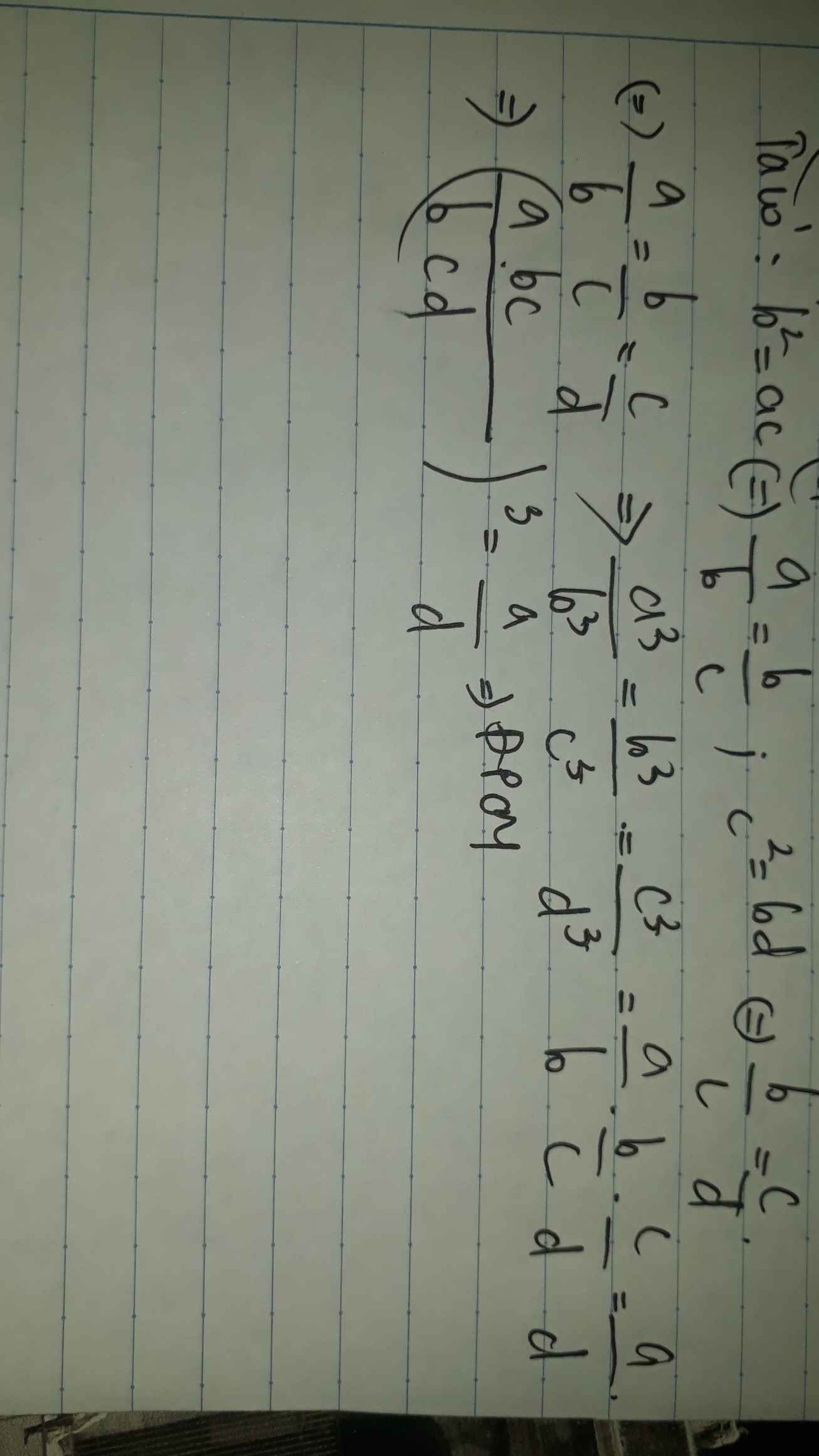
\(\Rightarrow\frac{ac}{bd}=\frac{a^2+c^2}{b^2+d^2}.\)
\(\Rightarrow\frac{ac}{a^2+c^2}=\frac{bd}{b^2+d^2}\left(đpcm\right).\)
Chúc bạn học tốt!
4 tháng 8 2016
Ta đặt: a/b = a/d =k
=> a = b.k, c=d.k
Ta có: a2 + a.c/c2 - a.c=b2 + b.d/d2 - b.d
Vế trái: => (b.k)2 + (b.k)(d.k)/(d.k)2 - (b.k)(d.k)
=> b2.k2 + k(b.d)/d2.k2 - k.(b.d)
Ta lược bỏ các chữ giống nhau, ta được:
=> b2/d2
Vế phải: b2 +b.d/d2 - b.d
Ta cũng lược bỏ những chữa giống nhau ta được:
=> b2/d2
Vậy a2 +a.c/c2 + a.c = b2 + b.d/d2 - b.d