Rút gọn rồi tính giá trị biêu thức:
a) I = s ( s 2 - t ) + t ( t 2 + s ) tại t = -1 và s = 1;
b) N = u 2 ( u - v ) - v ( v 2 - u 2 ) tại u = 0,5 và v = − 1 2 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn tự thay t và s mà đề cho vào rồi tính bình thường
còn câu cuối tương tự

a, \(I=s\left(s^2-t\right)+\left(t^2+s\right)=s^3-st+t^2+s\)
Thay t = -1 và s = 1 vào biểu thức trên ta được :
\(1+1+1+1=4\)
b, \(N=u^2\left(u-v\right)-v\left(v^2-u^2\right)=u^2\left(u-v\right)+v\left(u+v\right)\left(u-v\right)\)
\(=\left(u-v\right)\left(u^2+v\left(u+v\right)\right)\)
Thay \(u=0,5=\frac{1}{2};v=-\frac{1}{2}\)
\(=\left(\frac{1}{2}+\frac{1}{2}\right).\frac{1}{4}=\frac{1}{4}\)

Với t = 1, ta có s = 50.t - 8 = 50.1-8 = 42 (km)
Với t = 2, ta có s = 50.t - 8 = 50.2-8 = 92 (km)
Với t = 3, ta có s = 50.t - 8 = 50.3-8 = 142 (km)
Với t = 4, ta có s = 50.t - 8 = 50.4-8 = 92 (km)
.......
s là hàm số của t vì đại lượng s phụ thuộc vào đại lượng thay đổi t và với mỗi giá trị của t ta chỉ xác định được một giá trị tương ứng của s.

Với t = 1, ta có s = 50.t - 8 = 50.1-8 = 42 (km)
Với t = 2, ta có s = 50.t - 8 = 50.2-8 = 92 (km)
Với t = 3, ta có s = 50.t - 8 = 50.3-8 = 142 (km)
Với t = 4, ta có s = 50.t - 8 = 50.4-8 = 92 (km)
.......
s là hàm số của t vì đại lượng s phụ thuộc vào đại lượng thay đổi t và với mỗi giá trị của t ta chỉ xác định được một giá trị tương ứng của s.

Đáp án C
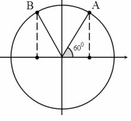
+ Dựa vào hình vẽ ta thấy tại thời điểm t ta có vị trí của điện áp cho giá trị
100
2
và đang giảm là ở A ® ![]()
+  s
s
+ Tại t = t 1 + 1 / 300 s = t 1 + T / 6 thì điện áp ở vị trí B.
® Góc quét từ A đến B là: 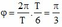 ® B đối xứng với A qua trục tung.
® B đối xứng với A qua trục tung.
® U = - 100 2 V

a) ĐKXĐ: \(x\ne0;x\ne-2\)
b) \(S=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{x+2-x^2}{x+2}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)\left(x+2-x^2\right)}{x}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{x^2+2x-x^3+2x+4-2x^2-x^2-6x-4}{x}\)
\(=\dfrac{-x^3-2x^2-2x}{x}\)
\(=\dfrac{x\left(-x^2-2x-2\right)}{x}\)
\(=-x^2-2x-2\)
Với \(x=0\Rightarrow\) loại
Với \(x=1\), thay vào \(S\) ta được
\(S=-1^2-2\cdot1-2=-5\)
c) Có: \(S=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)\)
\(=-\left(x^2+2x+1\right)-1\)
\(=-\left(x+1\right)^2-1\)
Ta thấy: \(\left(x+1\right)^2\ge0\forall x\ne0;x\ne-2\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\ne0;x\ne-2\)
\(\Rightarrow S=-\left(x+1\right)^2-1\le-1\forall x\ne0;x\ne-2\)
Dấu \("="\) xảy ra khi: \(x+1=0\Leftrightarrow x=-1\left(tmdk\right)\)
\(\text{#}\mathit{Toru}\)

a: tìm được 1 giá trị duy nhất tương ứng của s
b: Có thể tìm được 2 giá trị tương ứng của t
c:
| s | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 |
| t | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
a) Rút gọn I = s 3 + t 3 Þ I = 0.
b) Rút gọn N = u 3 – v 3 Þ N = 0.