Bài 1.
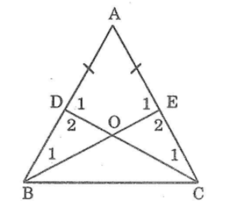
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, lấy điểm E trên cạnh AC sao cho AD = AE.
a) Chứng minh rằng BE = CD;
b) Gọi O là gia điểm của BE và CD. Chứng minh rằng △BOD =
△COE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé:
a) Xét tam giác ABE và tam giác ACD có:
AD = AE (gt)
A chung
AB = AC (gt)
Suy ra: tam giác ABE = tam giác ACD
(c - g - c)
=> BE = CD ( 2 cạnh tương ứng
a, xét xem tam giác ABE và tam giác ACD có:
AD=AE (gt)
A chung
AB=AC (gt)
suy ra tam giác abe = tam giác adc
=> BE=CD ( 2 cạnh tương ứng)

Xét ΔBEA và CDA, ta có:
BA = CA (giả thiết)
∠A chung
AE=AD (giả thiết)
Suy ra: ΔBEA = ΔCDA (c.g.c)
Vậy: BE = CD (hai cạnh tương ứng)

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác

a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC

a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
b: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Xét ΔBOD và ΔCOE có
\(\widehat{ODB}=\widehat{OEC}\)
DB=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔBOD=ΔCOE

AB = AC (gt)
=> Tam giác ABC cân tại A
Xét tam giác EAB và tam giác DAC có:
EA = DA (gt)
A chung
AB = AC (gt)
=> Tam giác EAB = Tam giác DAC (c.g.c)
=> EB = DC (2 cạnh tương ứng)
EBA = DCA (2 góc tương ứng)
mà ABC = ACB (tam giác ABC cân tại A)
=> ABC - EBA = ACB - DCA
hay EBC = DCB
=> Tam giác OBC cân tại O
Xét tam giác BOD và tam giác COE có:
DBO = ECO (tam giác EAB = tam giác DAC)
BO = CO (tam giác OBC cân tại O)
BOD = COE (2 góc đối đỉnh)
=> Tam giác BOD = Tam giác COE (c.g.c)
\(a,\left\{{}\begin{matrix}AB=AC\\AD=AE\\\widehat{BAC}\text{ chung}\end{matrix}\right.\Rightarrow\Delta AEB=\Delta ADC\left(c.g.c\right)\\ \Rightarrow BE=CD\\ b,\Delta AEB=\Delta ADC\\ \Rightarrow\widehat{ABE}=\widehat{ACD};\widehat{AEB}=\widehat{ADC}\\ \Rightarrow180^0-\widehat{AEB}=180^0-\widehat{ADC}\\ \Rightarrow\widehat{BDO}=\widehat{CEO}\\ \left\{{}\begin{matrix}\widehat{ABE}=\widehat{ACD}\\\widehat{BDO}=\widehat{CEO}\\BE=CD\end{matrix}\right.\Rightarrow\Delta BOD=\Delta COE\left(g.c.g\right)\)