Cho Hình 4.32, biết \(\widehat {OAB} = \widehat {ODC},OA = OD\) và \(AB = CD\).
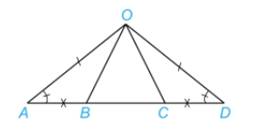
Chứng minh rằng:
a) \(AC = DB\);
b) \(\Delta OAC = \Delta ODB\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right)\)
Mà \(BC \in \left( {OBC} \right) \Rightarrow OA \bot BC\)
b) Ta có \(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right)\)
Mà \(CA \in \left( {OAC} \right) \Rightarrow CA \bot OB\)
c) Ta có \(\left. \begin{array}{l}OC \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OC \bot \left( {OAB} \right)\)
Mà \(AB \in \left( {OAB} \right) \Rightarrow AB \bot OC\)

`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`

\(a,Do\Delta\)vuông AHC có:
AH2=AE.AC (1)
\(\Delta\) vuông AHB có:
AH2=AD.AB (2)
Từ (1) và (2) :
AE.AC =AD.AB
b, Xest \(\Delta\)AED và \(\Delta\)ABC có:
\(\widehat{BAC}\)chung
AE.AC=AD.AB (câu a)
=> tam giác AED đồng dạng với tam giác ABC ( c-g-c)
=> Góc ADE = góc ACB ( điều phải chứng minh )
c, Do tam giác ADE đồng dạng với tam giác ABC
=> Góc E1 = Góc B1 (1)
Mà góc B1 + góc H1 = 90 độ ( tam giác BDH vuông tại D )
Góc H1 + Góc H2 = 90 độ ( tam giác AHB vuông tại D )
=> Góc B1 = Góc H2 (2)
Từ (1) và (2) : => Góc E1 = góc H2
Xét tam giác AOE và tam giác DOH có:
Góc O1 = Góc O2 ( 2 góc đối đỉnh )
Góc E1 = góc H2 ( chứng minh trên )
=> tam giác AOE đồng dạng với tam giác DOH (g-g)
=> \(\frac{OA}{OD}=\frac{OE}{OH}\)=> OA . OH = OD . OE

a)
Tam giác ABD và BCE là tam giác đều nên \(\widehat {EBC} = \widehat {DAB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc EBC và DAB ở vị trí đồng vị nên AD // BE.
Tam giác ABD và BCE là tam giác đều nên \(\widehat {DBA} = \widehat {ECB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc DBA và ECB ở vị trí đồng vị nên BD // CE.
b) Ta có A, B, C thẳng hàng nên góc ABC bằng 180°. Mà \(\widehat {DBA} = \widehat {EBC} = 60^\circ \Rightarrow \widehat {DBE} = 60^\circ \).
Vậy \(\widehat {ABE} = \widehat {DBC} = 120^\circ \) (\(\widehat {ABE} = \widehat {DBA} + \widehat {DBE};\widehat {DBC} = \widehat {DBE} + \widehat {EBC}\)).
c) Tam giác ABD và BCE là tam giác đều
\(\Rightarrow AB=AD, BE=BC\)
Xét hai tam giác ABE và DBC có:
AB = DB;
\(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
BE = BC.
\(\Rightarrow \Delta ABE = \Delta DBC\) (c.g.c)
Do đó, AE = DC ( 2 cạnh tương ứng).

a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)

a) Xét ΔBAD và ΔABC có
AB chung
\(\widehat{BAD}=\widehat{ABC}\)(gt)
AD=BC(gt)
Do đó: ΔBAD=ΔABC(c-g-c)
Suy ra: BD=AC(hai cạnh tương ứng)
Xét ΔADC và ΔBCD có
AD=BC(gt)
AC=BD(cmt)
DC chung
Do đó: ΔADC=ΔBCD(c-c-c)
Suy ra: \(\widehat{ADC}=\widehat{BCD}\)(hai góc tương ứng)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
\(\Leftrightarrow2\cdot\widehat{BAD}+2\cdot\widehat{ADC}=360^0\)
\(\Leftrightarrow\widehat{BAD}+\widehat{ADC}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
Xét tứ giác ABCD có AB//CD(cmt)
nên ABCD là hình thang(Định nghĩa hình thang)
Hình thang ABCD(AB//CD) có AC=BD(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
a) Ta có:
\(\begin{array}{l}AB = CD\\ \Rightarrow AB + BC = CD + BC\\ \Rightarrow AC = BD\end{array}\)
b) Xét tam giác OAC và ODB có:
\(AC=BD\) (cmt)
\(\widehat A = \widehat D\) (gt)
\(OA=OD\) (gt)
\(\Rightarrow \Delta OAC = \Delta ODB\)(c.g.c)