Giả sử hàm số \(f\left(x\right)\) liên tục trên đoạn \(\left[-a;a\right]\)
Chứng minh rằng :
\(\int\limits^a_{-a}f\left(x\right)dx=\left\{{}\begin{matrix}2\int\limits^a_0f\left(x\right)dx;nếuflàhàmchẵn\\0;nếuflàhàmlẻ\end{matrix}\right.\)
Áp dụng để...
Đọc tiếp
Giả sử hàm số \(f\left(x\right)\) liên tục trên đoạn \(\left[-a;a\right]\)
Chứng minh rằng :
\(\int\limits^a_{-a}f\left(x\right)dx=\left\{{}\begin{matrix}2\int\limits^a_0f\left(x\right)dx;nếuflàhàmchẵn\\0;nếuflàhàmlẻ\end{matrix}\right.\)
Áp dụng để tính \(\int\limits^2_{-2}\ln\left(x+\sqrt{1+x^2}\right)dx\)
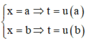
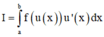
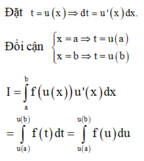
Tham khảo:
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
Đổi biến x = - t đối với tích phân
Ta được:
Vậy
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì
là hàm số lẻ trên đoạn [-2; 2] nên