A C B H a c' b' h b c
Chứng minh các hệ thức lượng;
a)\(b^2=ab'\).
b)\(h^2=b'c'\)
c)\(a-h=bc\)
d)\(\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 6 2019
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
20 tháng 8 2021
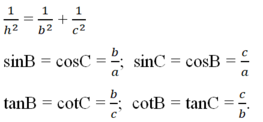
a: \(AB^2=HB^2+HA^2\)
\(BM\cdot BA=BH^2\)
\(AM\cdot AB=AH^2\)
\(BH\cdot HA=HM\cdot BA\)
\(HM^2=MA\cdot MB\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền BA, ta được:
\(BM\cdot BA=BH^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền BC, ta được:
\(BN\cdot BC=BH^2\)
Xét tứ giác BNHM có
\(\widehat{NBM}=\widehat{BNH}=\widehat{BMH}=90^0\)
Do đó: BNHM là hình chữ nhật
Suy ra: BH=NM
Ta có: \(BM\cdot BA+BN\cdot BC\)
\(=BH^2+BH^2\)
\(=2\cdot NM^2\)
20 tháng 8 2021
Bạn tự vẽ hình nha.
a) \(sinA=\dfrac{BH}{AB},cosA=\dfrac{AH}{AB},tanA=\dfrac{BH}{AH},cotA=\dfrac{AH}{BH}\\sin \widehat{ABH}=\dfrac{AH}{AB},cos\widehat{ABH}=\dfrac{BH}{AB},tan\widehat{ABH}=\dfrac{AH}{BH},cot\widehat{ABH}=\dfrac{BH}{AH}\)
b)Áp dụng định lí Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(CH=\sqrt{BC^2-BH^2}=\sqrt{900-576}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(AC=\dfrac{BC^2}{HC}=\dfrac{900}{18}=50\left(cm\right)\)
\(AB=\dfrac{BH\cdot AC}{BC}=\dfrac{24\cdot50}{30}=40\left(cm\right)\)
\(AH=\dfrac{AB^2}{AC}=\dfrac{400}{50}=8\)(cm)
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
BN.BC=\(BH^2\)
BM.BA=\(BH^2\)
Suy ra, BN.BC+BM.BA=2\(BH^2\)
Xét tứ giác BMHN có:
góc BMH = góc MBN = góc HNB = \(90^0\)
nên tứ giác BMHN là hình chữ nhật.
suy ra BH = MN .
Suy ra, BN.BC+BM.BA = 2.\(MN^2\)(đpcm)
DK
6 tháng 8 2018
Đáp án C
Xét các kết luận
I đúng, các loài E,G,H đều thuộc bậc dinh dưỡng cấp 4
II sai, các chuỗi thức ăn có loài C là ACEH; ACH,ADCEH,ADCH,ADCGH;ACGH
III đúng
IV đúng ADCEH,ADCGH là 2 chuỗi có nhiều mắt xích nhấ
NT
4
N
24 tháng 6 2017
Ta có: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\Leftrightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\Leftrightarrow\dfrac{a}{b}=\dfrac{c}{d}\)
DH
24 tháng 6 2017
Ta có:
\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\Rightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a+b+a-b}{c+d+c-d}=\dfrac{a+b-a+b}{c+d-c+d}\\ =\dfrac{2a}{2c}=\dfrac{2b}{2d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\rightarrow\) đpcm
Chúc bạn học tốt!!!
LD
0
14 tháng 11 2018
Sửa đề \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\left(h_a+h_b+h_c\right)\left(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}\right)\) \(\left(1\right)\)
Gọi S là diện tích tam giác \(\Rightarrow\)\(S=\frac{ah_a}{2}=\frac{bh_b}{2}=\frac{ch_c}{2}\)\(\Rightarrow\)\(a=\frac{2S}{h_a};b=\frac{2S}{h_b};c=\frac{2S}{h_c}\)
\(VT=\left(\frac{2S}{h_a}+\frac{2S}{h_b}+\frac{2S}{h_c}\right)\left(\frac{1}{\frac{2S}{h_a}}+\frac{1}{\frac{2S}{h_b}}+\frac{1}{\frac{2S}{h_c}}\right)\) ( thay vào là xong )
\(VT=2S\left(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}\right)\left(\frac{h_a+h_b+h_c}{2S}\right)=\left(h_a+h_b+h_c\right)\left(\frac{1}{h_a}+\frac{1}{h_b}+\frac{1}{h_c}\right)\) ( đpcm )
Chúc bạn học tốt ~
6 tháng 9 2022
a: Xét ΔADC có M,P lần lượt là trung điểm của AD và AC
nên MP là đườn trung bình
=>MP//DC(1)
Xét ΔDAB có M,N lần lượt là trung điểm của AD và DB
nên MN là đường trung bình
=>MN//AB
=>MN//CD(2)
Xét hình thang ABCD có
M,Q lần lượt là trung điểm của AD và BC
nên MQ là đường trung bình
=>MQ//CD//AB(3)
Từ (1), (2) và (3) suy ra M,N,P,Q thẳng hàng
b: Xét tứ giác ABPN có AB//PN
nên ABPN là hình thang
a) Δ AHC ~ Δ CAB (g.g)
vì: \(\hept{\begin{cases}\widehat{C}:chung\\\widehat{AHC}=\widehat{BAC}=90^0\end{cases}}\)
=> \(\frac{HC}{AC}=\frac{AC}{BC}\Leftrightarrow HC\cdot BC=AC^2\Rightarrow b^2=ab'\)
b) Δ AHB ~ Δ CHA (g.g)
vì: \(\hept{\begin{cases}\widehat{ACH}=\widehat{BAH}=\left(90^0-\widehat{HAC}\right)\\\widehat{AHC}=\widehat{AHB}=90^0\end{cases}}\)
=> \(\frac{BH}{AH}=\frac{AH}{HC}\Leftrightarrow AH^2=HB\cdot HC\Rightarrow h^2=b'c'\)
c) \(S_{ABC}=\frac{1}{2}AH\cdot BC=\frac{1}{2}AB\cdot AC\)
\(\Rightarrow AH\cdot BC=AB\cdot AC\Rightarrow ah=bc\)
d) \(\frac{1}{b^2}+\frac{1}{c^2}=\frac{b^2+c^2}{b^2c^2}=\frac{a^2}{a^2h^2}=\frac{1}{h^2}\) (theo c)
chị lớp 9 em có lớp 7 thui em k biết nha