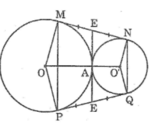
Qua điểm A ngoài đường tròn (O;R) vẽ 2 tiếp tuyến AB, AC với đường tròn(B,C là tiếp điểm)
A) chứng minh : AO là đường trung trực của BC
b) gọi H là giao điểm của AO và BC. Chứng minh AH.HO=BH.CH
c) AO cắt đường tròn (O;R) tại I và K(I nằm giữa A và O), Chứng minh AI.KH= IH.KA
Chỉ cần bài giải câu c) không cần trình bày câu a,b vì những câu đó dùng làmkết quả cho câu dưới