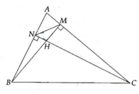
Cho tam giác nhọn ABC không cân nội tiêp (O;R), có H là trực tâm. I, K làn lượt là đường cao kẻ từ A, B. M là trung điểm BC. Kẻ HJ vuông góc với AM.
a) Cm: Góc IHK = góc MJK
b) Cm: \(\Delta AJK\) đồng dạng với \(\Delta ACM\)
c) Cm: MJ . MA < R2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2019
Xét tứ giác AMHN có: A M H ^ + A N H ^ = 90 0 + 90 0 = 180 0 => Đpcm
Xét tứ giác BNMC có: B N C ^ = B M C ^ = 90 0 => Đpcm
3 tháng 7 2023
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b; góc ABD=1/2*180=90 độ
=>BD vuông góc AB
=>BD//CH
góc ACD=1/2*180=90 độ
=>CD vuông góc AC
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
=>BHCD là hbh
=>BC cắt HDtại trung điểm của mỗi đường
=>H,M,D thẳng hàng
2 tháng 3 2023
a: Xét tứ giác HMCN co
góc HMC+góc HNC=180 đô
=>HMCN là tứ giác nội tiếp
b: góc CBE=1/2*sđ cung CE
góc CAD=1/2*sđ cung CD
mà góc CBE=góc CAD
nên CE=CD
c: góc BHD=góc ACB=1/2*sđ cung AB=góc BDH
=>ΔBHD cân tại B
16 tháng 3 2023
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B
2 tháng 3 2023
a: Xét tứ giác AKIB có
góc AKB=góc AIB=90độ
=>AKIB là tứ giác nội tiếp
b: góc BHD=góc AHE=90 độ-góc HAC=90 độ-1/2*sđ cung CD
góc BDH=90 độ-góc IBD=90 độ-1/2*sđ cung CD
=>góc BHD=góc BDH
=>ΔBHD cân tại B