Cho hình thang cân MNPQ(MN//PQ;MN<PQ).NP=15cm,đường cao NI=12cm,QI=16cm a)tính IP b)chứng minh QN vuông góc NP c)tính diện tích hình thang MNPQ d)gọi E là trung điểm của PQ.Đường thẳng vuông góc với EN tại N cắt đường thẳng PQ tại k.chứng minh KN2=KP.KQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Hình thang MNPQ có MP=NQ
nên MNPQ là hình thang cân
b: Xét tứ giác MNKP có
MN//KP
MP//KN
Do đó: MNKP là hình bình hành
Suy ra: MP=NK
mà MP=NQ
nên NK=NQ
hay ΔNKQ cân tại N

Đáp án cần chọn là: C
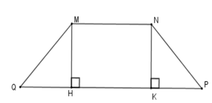
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 12 cm nên QH = KP = 40 − 12 2 = 14 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 12 + 40 ) .14 2 = 364 c m 2

Đáp án cần chọn là: B
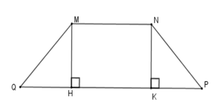
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNHK có MN // HK nên MNHK là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNKP (ch – cgv)
=> QH = KP = Q P − H K 2
Mà HK = MN = 8 cm nên QH = KP = 30 − 8 2 = 8 cm
Mà M Q P ^ = 45 ° => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = ( M N + P Q ) . M H 2 = ( 8 + 30 ) .11 2 = 209 c m 2 .

a: Xét tứ giác MNKP có
MN//KP
MP//NK
=>MNKP là hình bình hành
=>MP=NK
mà MP=NQ
nên NK=NQ
=>ΔNKQ cân tại N
b: MNKP là hbh
=>góc K=góc NMP
=>góc K=góc MPQ
=>góc MPQ=góc NQP
Xét ΔMQP và ΔNPQ có
MP=NQ
góc MPQ=góc NQP
QP chung
=>ΔMQP=ΔNPQ
c: ΔMQP=ΔNPQ
=>góc MQP=góc NPQ
=>MNPQ là hình thang cân

ΔNIQ vuông tại I
=>\(NI^2+IQ^2=NQ^2\)
=>\(NQ^2=12^2+16^2=400\)
=>\(NQ=\sqrt{400}=20\)
Ta có: MNPQ là hình thang cân
=>MQ=NP
mà NP=15
nên MQ=15
Ta có: QP=QI+IP
=16+9
=25
Kẻ MK\(\perp\)PQ tại K
Xét ΔMKQ vuông tại K và ΔNIP vuông tại I có
MQ=NP
\(\widehat{MQK}=\widehat{NPI}\)
Do đó: ΔMKQ=ΔNIP
=>QK=IP=9cm
Ta có: QK+KI=QI
=>KI+9=16
=>KI=7(cm)
Xét tứ giác MNIK có
MN//IK
MK//IN
Do đó: MNIK là hình bình hành
=>MN=KI
mà KI=7cm
nên MN=7cm

PQ=7*2=14cm
\(S_{MNPQ}=\dfrac{1}{2}\cdot\left(7+14\right)\cdot4=2\cdot21=42\left(cm^2\right)\)