cho tâm giác cân ABC vuông tại tại a .Trên cạnh BC lấy 2 điểm D và E theo thứ tự H;B;D;E sao cho góc DAE=45 độ
Chứng minh BD^2+CE^2=DE^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 8 2017
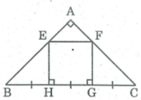
Vì ΔABC vuông cân tại A nên ∠ B = ∠ C = 45 0
Vì ΔBHE vuông tại H có ∠ B = 45 0 nên ΔBHE vuông cân tại H.
Suy ra HB = HE
Vì ΔCGF vuông tại G, có ∠ C = 45 0 nên ΔCGF vuông cân tại G
Suy ra GC = GF
Ta có: BH = HG = GC (gt)
Suy ra: HE = HG = GF
Vì EH // GF (hai đường thẳng cũng vuông góc với đường thắng thứ ba) nên tứ giác HEFG là hình bình hành (vì có một cặp cạnh đối song song bằng nhau);
Lại có ∠ (EHG) = 90 0 nên HEFG là hình chữ nhật.
Mà EH = HG (chứng minh trên).
Vậy HEFG là hình vuông.
30 tháng 6 2017
Tam giác vuông FGC có \(\widehat{C}=45^0\) nên là tam giác vuông cân. Do đó FG = GC
24 tháng 11 2023
1:
ΔABC vuông cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=45^0\)
EH\(\perp\)BC tại H
=>EH\(\perp\)HB tại H
=>ΔEHB vuông tại H
Xét ΔHEB vuông tại H có \(\widehat{HBE}=45^0\)
nên ΔHEB vuông cân tại H
FG\(\perp\)BC tại G
=>FG\(\perp\)GC tại G
=>ΔFGC vuông tại G
Xét ΔFCG vuông tại G có \(\widehat{GCF}=45^0\)
nên ΔFCG vuông cân tại G
2: EH\(\perp\)BC
FG\(\perp\)BC
Do đó: EH//FG
EH=HB
HB=HG=GC
GF=GC
Do đó; EH=HB=GH=CG=GF
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHFG là hình bình hành
Hình bình hành EHFG có \(\widehat{EHG}=90^0\)
nên EHFG là hình chữ nhật
Hình chữ nhật EHFG có GH=GF
nên EHFG là hình vuông
6 tháng 12 2018
hình như trên
+)Ta có: ( g-c-g) ( Vì cùng bằng )
Nên MD = NE.
+)Xét và :
( Hai góc đối đỉnh)
Nên ( cgv - gn)
+)Từ B và C kẻ các đường thẳng lần lượt vuông
Góc với AB và AC cắt nhau tại J.
Ta có:
Nên J thuộc AL đường trung trực ứng với BC
Mặt khác : Từ ( Câu a)
Ta có : BM = CN
BJ = CJ ( cm trên)
Nên ( c-g-c)
hay đường trung trực của MN
Luôn đi qua điểm J cố định.
20 tháng 3 2021
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(Hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
20 tháng 3 2021
vì ∠ACB +∠ACE=180o(2 góc kề bù)
=>∠ACE=180o-∠ACB
mà ∠ABC=∠ACB(ΔABC cân tại A)
=>∠ACE=∠ABD=180o-∠ACB
Xét ΔABD và ΔACE có:
AB=AC(ΔABC cân tại A)
BD=CE(giả thuyết)
∠ABD=∠ACE(chứng minh trên)
=>ΔACE=ΔABD(C-G-C)
=>ΔADE cân tại A
vì M là trung điểm của BC nên MC=MB
mà BD=CE(giả thuyết)
=>ME=MD
xét ΔAME và ΔAMD có:
AM là cạnh chung
AE=AD(câu a)
ME=MD(chứng minh trên)
=>ΔAMD=ΔAME(C-C-C)
=> ∠DAM=∠EAM(2 góc tưng ứng)
=>AM là tia phân giác của ∠DAE
ta có:∠CAE=∠BAD(câu a)
=>∠BAH=∠CAK=∠BAC+∠CAH
xét 2 tam giác vuông AHB và AKC có:
AB=AC(Δ ABC cân tại A)
∠CAK=∠BAH(chứng minh trên)
=>ΔBAH=ΔCAK(cạnh-huyền-góc-nhọn)
=>BH=CK(2 cạnh tưng ứng)
Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm