Cho hình thang vuông ABCDco AB = 15cm;DC = 20cm;AD = 12cm. Trong hình thang có hình tam giác BMN. Tính diện tích hình tam giác BMN, biết AM = MD và ĐN =10 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 7 2021
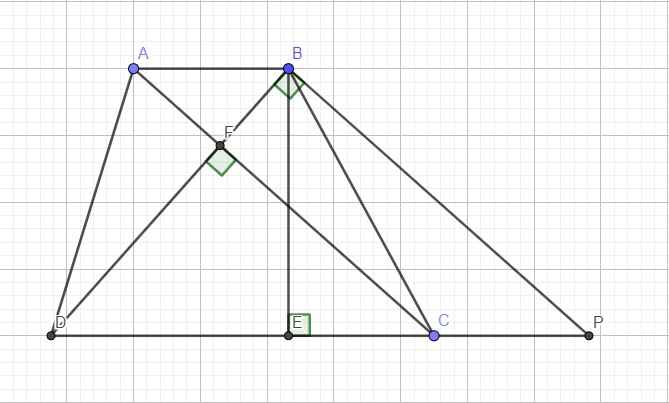
Kẻ đường cao BE \(\Rightarrow BE=12\)
Pitago tam giác vuông BDE:
\(DE=\sqrt{BD^2-BE^2}=9\left(cm\right)\)
Qua B kẻ đường thẳng song song AC cắt CD kéo dài tại P
Do \(AC\perp BD\Rightarrow BP\perp BD\) hay tam giác BPD vuông tại B
Mặt khác \(\left\{{}\begin{matrix}AB||CD\\AC||BP\end{matrix}\right.\) \(\Rightarrow ABPC\) là hbh
\(\Rightarrow AB=CP\Rightarrow AB+CD=CP+CD=DP\)
Hệ thức lượng tam giác vuông BPD:
\(BD^2=DE.DP\Rightarrow DP=\dfrac{BD^2}{DE}=25\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}BE.\left(AB+CD\right)=\dfrac{1}{2}BE.DP=\dfrac{1}{2}.9.25=112,5\left(cm^2\right)\)
23 tháng 10 2021
Áp dụng PTG: \(AD=\sqrt{AC^2-AD^2}=\sqrt{17^2-15^2}=8\left(cm\right)\)
Kẻ đg cao BH
Do đó \(\widehat{BAD}=\widehat{ADH}=\widehat{DHB}=90^0\) nên ABHD là hcn
Do đó \(AB=DH=9\left(cm\right);AD=BH=8\left(cm\right)\)
\(\Rightarrow HC=CD-DH=17-9=8\left(cm\right)\)
Áp dụng PTG cho tg BHC vuông tại H
\(BC=\sqrt{BH^2+CH^2}=\sqrt{64+64}=8\sqrt{2}\left(cm\right)\)
Vậy độ dài các cạnh bên AD,BC là 8 cm và \(8\sqrt{2}\) cm
29 tháng 12 2022
Theo đề là CD=15cm mà ở dòng 10 cậu có bị nhầm với AC sau khiến những câu dưới bị sai ạ
co ai biet lam ko lam on lam nhanh len cho minh voi minh cho