Từ điêm A nằm ngoài đường tròn (O) tã vẽ tiếp tuyến AB và cắt tuyến ACD với đường tròn sao cho tia AO nằm giữa AB và AD (B:tiếp điểm;C nằm giữa A và D).Gọi M là trung điểm của CD. a) cm AB^2=AC×AD b) cm tứ giác ABOM nt đường tròn (I) . ĐỊNH TÂM I c) đường tròn I cắt đường tròn O tại E. Cm AE là tiếp tuyến của đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xet ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
=>AD/AO=AH/AE
=>ΔADH đồng dạng với ΔAOE
=>góc ADH=góc AOE
=>góc DHO+góc DEO=180 độ
=>DEOH nội tiếp
=>góc EHO=góc EDO

a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)

a:
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC
c: Xét (O) có
ΔBCN nội tiếp
BN là đường kính
Do đó: ΔBCN vuông tại C
=>BC\(\perp\)CN
Ta có: BC\(\perp\)CN
BC\(\perp\)OA
Do đó: OA//CN


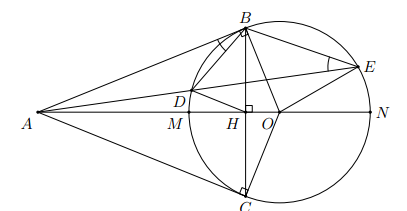
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube

a: góc ABH=góc ABM=1/2*sđ cung BM
góc AEB=1/2(sđ cung BC+sđ cung DM)
=1/2(sđ cung BC+sđ cung MC)
=1/2*sđ cung BM
=>góc AEB=góc ABE
=>ΔABE cân tại A
mà AH là phân giác
nên AH vuông góc với BE
b: Xét ΔMDE và ΔMBD có
góc MDE=góc MBD
góc DME chung
Do đó: ΔMDE đồng dạng với ΔMBD
=>MD/MB=ME/MD
=>MD^2=MB*ME

a: góc AEB=(sd cung BC+sđ cung DM)/2
=1/2(sđ cung BC+sđ cung CM)
=1/2*sđ cung BM
=góc ABM
=góc ABE
=>ΔABE cân tại A
mà AH là phân giác
nen AH vuông góc với BE
b: Xét ΔMDE và ΔMBD có
góc MDE=góc MBD
góc DME chung
=>ΔMDE đồng dạng với ΔMBD
=>MD/MB=ME/MD
=>MD^2=MB*ME
 hình
hình
a: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
=>ΔABC đòng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
b: góc AMO=góc ABO=90 độ
=>ABMO nội tiếp, I là trung điểm của AO