Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với \(AB=a;BC=a\sqrt{3}\), H là trung điểm của cạnh AB. Biết 2 mặt phẳng (SHC) và (SHD) cùng vuông góc với mặt phẳng (ABCD), đường thẳng SD tạo với mặt đáy góc 60 độ. Tính thể tích khối chóp và khoảng cách giữa 2 đường thẳng AC và SB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
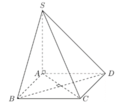
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3

Đáp án B
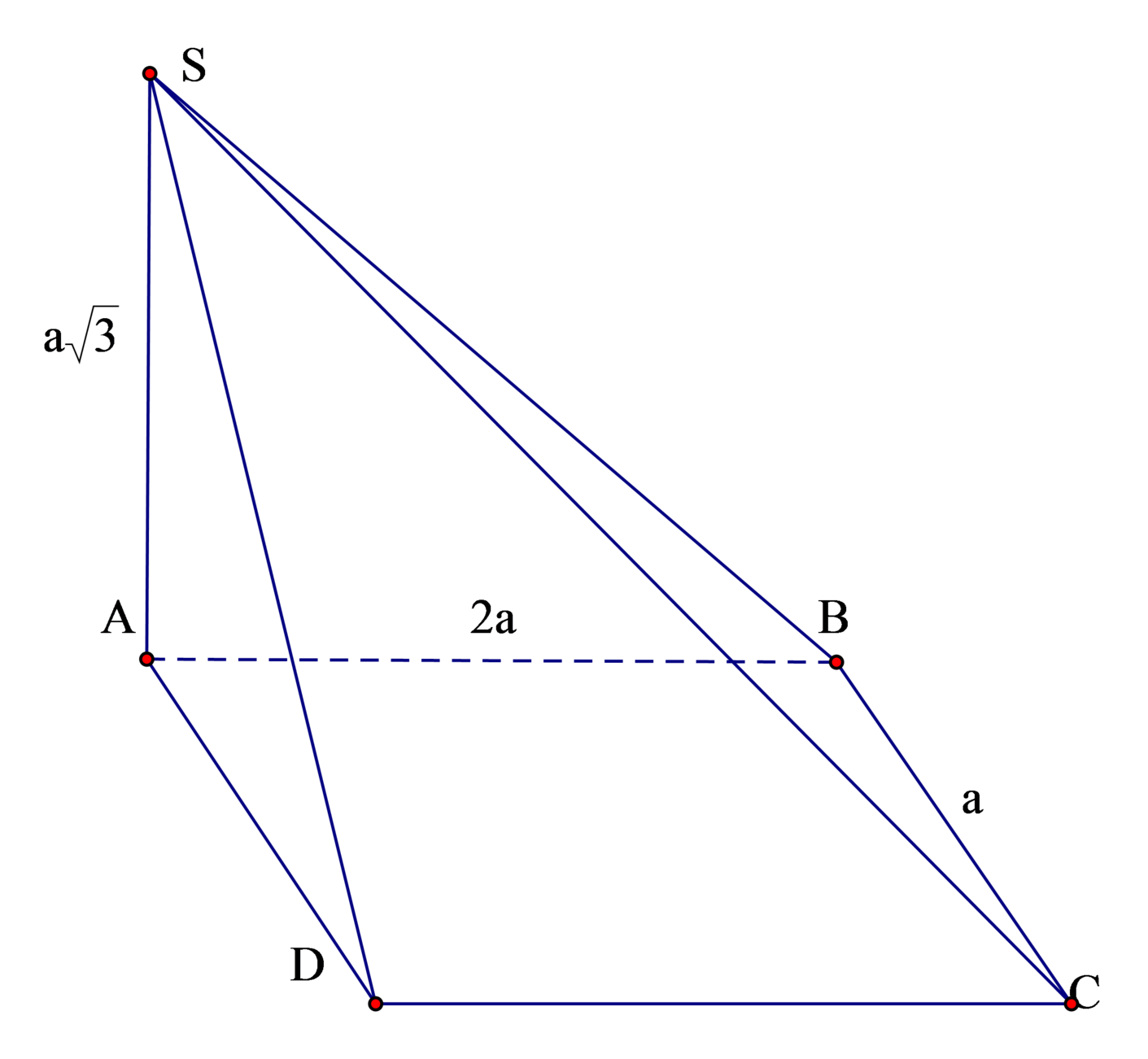
Do S A ⊥ A B C D
⇒ V S A B C D = 1 3 S A . d t A B C D = 1 3 S A . A B . B C = 1 3 a 3 .2 a . a = 2 a 3 3 3

Đáp án B
Thể tích khối chóp là
V = 1 3 S A . S A B C D = 1 3 . a . 3 .2 a . a = 2 a 3 3 3

Đáp án B
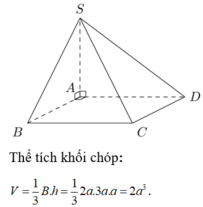
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3


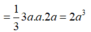

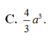
Ta có \(\left(SHC\right)\cap\left(SHD\right)=SH\)
Từ giả thiết \(\left(SHC\right)\perp\left(ABCD\right);\left(SHD\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(\Leftrightarrow V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}AB.AD.SH=\frac{1}{3}a^2\sqrt{3}.SH\left(1\right)\)
Ta có \(SH\perp\left(ABCD\right)\Rightarrow HD\) là hình chiếu của SD trên (ABCD), suy ra góc giữa SD và (ABCD) là \(\widehat{SDH}=60^0\Rightarrow SH=HD\tan\widehat{SDHH}=\frac{a\sqrt{39}}{2}\)
Khi đó \(V_{S.ABCD}=\frac{1}{2}a^3\sqrt{13}\)
Dựng hình bình hành ACBE. Khi đó AC//BE suy ra AC//(SBE)
\(\Rightarrow d\left(AC,SB\right)=d\left(AC,\left(SBE\right)\right)=d\left(A,\left(SBE\right)\right)=2d\left(H,\left(SBE\right)\right)\)
Gọi K, I lần lượt là hình chiếu của H trên BE và SK.
Khi đó \(BE\perp KH,BE\perp SH\Rightarrow BE\perp HI\left(1\right)\)
Mặt khác \(HI\perp SK\left(2\right)\)
Từ (1) và (2) suy ra \(HI\perp\left(SBE\right)\Rightarrow d\left(H,\left(SBE\right)\right)=HI\)
Tính được \(HK=\frac{a\sqrt{3}}{4};HI=\frac{a\sqrt{39}}{\sqrt{212}}\)
\(\Rightarrow d\left(AC,SB\right)=2d\left(H,\left(SBE\right)\right)=2HI=\frac{a\sqrt{39}}{\sqrt{53}}=\frac{a\sqrt{2067}}{53}\)
Ý C